
已知函數f(x)的定義域為R,且滿足f(x+2)=-f(x)?.
(1)求證:f(x)是周期函數;
(2)若f(x)為奇函數,且當0≤x≤1時,f(x)=![]() x,求使f(x)=-
x,求使f(x)=-![]() 在[0,2 009]上的所有x的個數.
在[0,2 009]上的所有x的個數.
(1)證明見解析(2)在[0,2 009]上共有502個x使f(x)=- ![]()
(1)證明 ∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=-[-f(x)]=f(x), 2分
∴f(x)是以4為周期的周期函數, 4分
(2)解 當0≤x≤1時,f(x)=![]() x,
x,
設-1≤x≤0,則0≤-x≤1,∴f(-x)=![]() (-x)=-
(-x)=-![]() x.
x.
∵f(x)是奇函數,∴f(-x)=-f(x),
∴-f(x)=-![]() x,即f(x)=
x,即f(x)=![]() x. 7分
x. 7分
故f(x)= ![]() x(-1≤x≤1) 8分
x(-1≤x≤1) 8分
又設1<x<3,則-1<x-2<1,
∴f(x-2)= ![]() (x-2), 10分
(x-2), 10分
又∵f(x-2)=-f(2-x)=-f((-x)+2)=-[-f(-x)]=-f(x),
∴-f(x)=![]() (x-2),
(x-2),
∴f(x)=-![]() (x-2)(1<x<3). 11分
(x-2)(1<x<3). 11分
∴f(x)=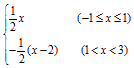 12分
12分
由f(x)=- ![]() ,解得x=-1.
,解得x=-1.
∵f(x)是以4為周期的周期函數.
∴f(x)=- ![]() 的所有x=4n-1 (n∈Z). 14分
的所有x=4n-1 (n∈Z). 14分
令0≤4n-1≤2 009,則![]() ≤n≤
≤n≤![]() ,
,
又∵n∈Z,∴1≤n≤502 (n∈Z),
∴在[0,2 009]上共有502個x使f(x)=- ![]() . 16分
. 16分


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:
| 1 |
| 3 |
| a-3 |
| 2 |
| x | 2 1 |
| x | 2 2 |
| x | 3 1 |
| x | 3 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
| 1+x |
| 1 |
| 10 |
| 1 |
| 9 |
| 1 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| x |
| ||
1+
|
| x |
| 1+x |
| 1 |
| 1+x |
| x |
| 1+x |
| 1+x |
| 1+x |
| 1 | ||
2x+
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 1-x |
| 1 |
| 2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| lim |
| n→∞ |
| 4Sn-9Sn |
| 4Sn+1+9Sn+1 |
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| x+1-a |
| a-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com