分析:(Ⅰ)利用線面、面面垂直的判定定理即可證明;
(Ⅱ)通過建立空間直角坐標系,利用兩平面的法向量的夾角即可得到二面角.
解答:證明:(Ⅰ)由側面AA
1B
1B為正方形,知AB⊥BB
1.
又AB⊥B
1C,BB
1∩B
1C=B
1,∴AB⊥平面BB
1C
1C,
又AB?平面AA
1B
1B,∴平面AA
1B
1B⊥BB
1C
1C.
(Ⅱ)由題意,CB=CB
1,設O是BB
1的中點,連接CO,則CO⊥BB
1.
由(Ⅰ)知,CO⊥平面AB
1B
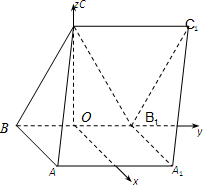
1A.建立如圖所示的坐標系O-xyz.
其中O是BB
1的中點,Ox∥AB,OB
1為y軸,OC為z軸.
不妨設AB=2,則A(2,-1,0),B(0,-1,0),C(0,0,
),A
1(2,1,0).
=(-2,0,0),
=(-2,1,
),
=(0,2,0).
設
=(x
1,y
1,z
1)為面ABC的法向量,則
•
=0,
•
=0,
即
取z
1=-1,得
=(0,
,-1).
設
=(x
2,y
2,z
2)為面ACA
1的法向量,則
•
=0,
•
=0,
即
取x
2=
,得
=(
,0,2).
所以cos?n
1,n
2>=
=-
.
因此二面角B-AC-A
1的余弦值為-
.
點評:熟練掌握線面、面面垂直的判定定理、通過建立空間直角坐標系并利用兩平面的法向量的夾角求二面角的方法是解題的關鍵.

 如圖,三棱柱ABC-A1B1C1的側面AA1B1B為正方形,側面BB1C1C為菱形,∠CBB1=60°,AB⊥B1C.
如圖,三棱柱ABC-A1B1C1的側面AA1B1B為正方形,側面BB1C1C為菱形,∠CBB1=60°,AB⊥B1C.


 如圖,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分別為AA1、B1C的中點,AB=AC.
如圖,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分別為AA1、B1C的中點,AB=AC. (2012•黑龍江)如圖,三棱柱ABC-A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龍江)如圖,三棱柱ABC-A1B1C1中,側棱垂直底面,∠ACB=90°,AC=BC= 如圖,三棱柱ABC-A1B1C1的底面ABC為正三角形,側棱AA1⊥平面ABC,D是BC中點,且AA1=AB
如圖,三棱柱ABC-A1B1C1的底面ABC為正三角形,側棱AA1⊥平面ABC,D是BC中點,且AA1=AB (2012•大連二模)如圖,三棱柱ABC-A′B′C′,cc′=
(2012•大連二模)如圖,三棱柱ABC-A′B′C′,cc′=