
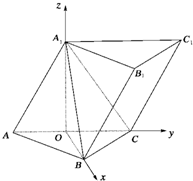
 如圖,已知三棱柱ABC-A1B1C1的側棱與底面所成的角為60°,AB=BC,A1A=A1C=2,AB⊥BC,側面AA1C1C⊥底面ABC.
如圖,已知三棱柱ABC-A1B1C1的側棱與底面所成的角為60°,AB=BC,A1A=A1C=2,AB⊥BC,側面AA1C1C⊥底面ABC.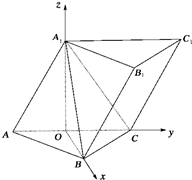 解:取AC中點為O,由A1A=A1C,AB=BC,知A1O⊥AC,BO⊥AC,
解:取AC中點為O,由A1A=A1C,AB=BC,知A1O⊥AC,BO⊥AC, ),C(0,1,0).
),C(0,1,0).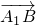 =(1,0,-
=(1,0,- ),
), =
= =(0,2,0)
=(0,2,0)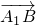 •
• =0
=0 =(x,y,z)為面BCC1的一個法向量.
=(x,y,z)為面BCC1的一個法向量. =(-1,1,0),
=(-1,1,0),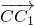 =
=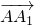 =(0,1,
=(0,1, )
) •
• =
= •
•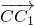 =0,
=0,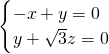 取n=(
取n=( ,
, ,-1).
,-1). =(1,0,0)是面ACC1的法向量,
=(1,0,0)是面ACC1的法向量, ,
, >=
>= =
=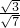 =
=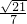 .
.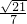 .
. A1A=
A1A= ,球表面積S=4πR2=
,球表面積S=4πR2= π.
π.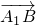 ⊥
⊥ 即說明
即說明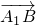 •
• =0即可故需求出
=0即可故需求出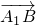 ,
, 的坐標然后利用平面向量數量積的坐標計算求出
的坐標然后利用平面向量數量積的坐標計算求出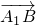 •
• 即可.
即可. ,
, >=
>= 求出<
求出< ,
, >而點B在平面ACC1內的射影O在二面角的面ACC1內故二面角A-CC1-B為銳角所以二面角A-CC1-B的大小為<
>而點B在平面ACC1內的射影O在二面角的面ACC1內故二面角A-CC1-B為銳角所以二面角A-CC1-B的大小為< ,
, >(cos<
>(cos< ,
, >>0)或π-<
>>0)或π-< ,
, >(cos<
>(cos< ,
, ><0).
><0).

科目:高中數學 來源: 題型:
 如圖,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,AB=2
如圖,已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AC=BC=2,AA1=4,AB=2| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知三棱柱ABC-A1B1C1的側棱與底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中點,N是BC的中點,點P在直線A1B1上,且滿足
如圖,已知三棱柱ABC-A1B1C1的側棱與底面垂直,AA1=AB=AC=1,且AB⊥AC,M是CC1的中點,N是BC的中點,點P在直線A1B1上,且滿足| A1P |
| A1B1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知三棱柱ABC-A1B1C1的側棱與底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分別是CC1,BC的中點,點P在直線A1B1上,且
如圖,已知三棱柱ABC-A1B1C1的側棱與底面垂直,AA1=AB=AC=1,AB⊥AC,M,N分別是CC1,BC的中點,點P在直線A1B1上,且| A1P |
| A1B1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D為AC中點.
如圖,已知三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=BC,∠ABC=90°,D為AC中點.| 2 |
| 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com