
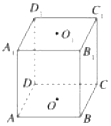
 如圖所示,在正方體ABCD-A1B1C1D1中,O1、O為上、下底面的中心,在直線D1D、A1D、A1D1、C1D1、O1D與平面AB1C平行的直線有2條.
如圖所示,在正方體ABCD-A1B1C1D1中,O1、O為上、下底面的中心,在直線D1D、A1D、A1D1、C1D1、O1D與平面AB1C平行的直線有2條. 分析 DD1與平面AB1C相交;由A1D∥B1C,知A1D∥平面AB1C;A1D1與平面AB1C相交;C1D1與平面AB1C相交;由O1D∥OB1,知O1D∥平面AB1C.
解答 解:在正方體ABCD-A1B1C1D1中,O1、O為上、下底面的中心,
∵DD1∥BB1,BB1∩平面AB1C=B1,
∴DD1與平面AB1C相交;
∵A1D∥B1C,AD1?平面AB1C,B1C?平面AB1C,∴A1D∥平面AB1C;
A1D1∥B1C1,B1C1∩平面AB1C=B1,
∴A1D1與平面AB1C相交;
∵C1D1∥A1B1,A1B1∩平面AB1C=B1,
∴C1D1與平面AB1C相交;
∵O1D∥OB1,OB1?平面AB1C,
∴O1D∥平面AB1C.
∴在直線D1D、A1D、A1D1、C1D1、O1D與平面AB1C平行的直線有2條.
故答案為:2.
點評 本題考查直線與平行的位置關系的判斷,是中檔題,解題時要認真審題,注意空間思維能力的培養.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:解答題
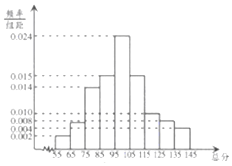 從某市統考的學生數學考試卷中隨機抽查100份數學試卷作為樣本,分別統計出這些試卷總分,由總分得到如下的頻率分布直方圖.
從某市統考的學生數學考試卷中隨機抽查100份數學試卷作為樣本,分別統計出這些試卷總分,由總分得到如下的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?n∈N,3n<n2+1 | B. | $?{n_0}∈N,{3^{n_0}}<n_0^2+1$ | ||
| C. | ?n∈N,3n≤n2+1 | D. | $?{n_0}∈N,{3^{n_0}}≥n_0^2+1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 銳角三角形 | B. | 鈍角三角形 | C. | 直角三角形 | D. | 斜三角形 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com