
【題目】某人經營淡水池塘養草魚,根據過去![]() 期的養殖檔案,該池塘的養殖重量
期的養殖檔案,該池塘的養殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的
百斤的![]() 期,不低于
期,不低于![]() 百斤且不超過
百斤且不超過![]() 百斤的有
百斤的有![]() 期,超過
期,超過![]() 百斤的有
百斤的有![]() 期.根據統計,該池塘的草魚重量的增加量
期.根據統計,該池塘的草魚重量的增加量![]() (百斤)與使用某種餌料的質量
(百斤)與使用某種餌料的質量![]() (百斤)之間的關系如圖所示.
(百斤)之間的關系如圖所示.
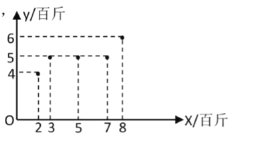
魚的重量(單位:百斤) |
|
|
|
沖水機運行臺數 | 1 | 2 | 3 |
(1)根據數據可知![]() 與
與![]() 具有線性相關關系,請建立
具有線性相關關系,請建立![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;如果此人設想使用某種餌料
;如果此人設想使用某種餌料![]() 百斤時,草魚重量的增加量須多于
百斤時,草魚重量的增加量須多于![]() 百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
(2)養魚的池塘對水質含氧與新鮮度要求較高,故養殖戶需設置若干臺增氧沖水機,每期養殖使用的沖水機運行臺數與魚塘的魚重量有關,并有如下關系:
若某臺增氧沖水機運行,則該臺沖水機每期盈利![]() 千元;若某臺沖水機未運行,則該臺沖水機每期虧損
千元;若某臺沖水機未運行,則該臺沖水機每期虧損![]() 千元.以頻率 作為概率,養殖戶欲使每期沖水機總利潤的均值達到最大,應安裝幾臺增氧沖水機?
千元.以頻率 作為概率,養殖戶欲使每期沖水機總利潤的均值達到最大,應安裝幾臺增氧沖水機?
附:對于一組數據![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計公式分別為:
的斜率和截距的最小二乘估計公式分別為: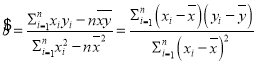 ,
,![]() .
.
【答案】(1)不可行,理由見解析(2)![]() 臺沖水機
臺沖水機
【解析】
(1)分別計算出![]() ,然后根據公式即可計算出
,然后根據公式即可計算出![]() 的值,再根據
的值,再根據![]() 即可求解出
即可求解出![]() 的值,從而可求回歸方程,再進行相關判斷;
的值,從而可求回歸方程,再進行相關判斷;
(2)分類討論沖水機的臺數:![]() ,分別計算出對應的利潤期望值進行大小比較,即可分析出應該安裝幾臺沖水機.
,分別計算出對應的利潤期望值進行大小比較,即可分析出應該安裝幾臺沖水機.
(1)由已知數據可得![]() ,
,![]() ,
,
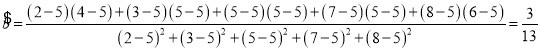 ,
,
![]() ,故
,故![]() ,
,
當![]() 時,
時,![]() ,故該方案不可行;
,故該方案不可行;
(2)記養殖戶每期設置沖水機的總利潤為![]() 千元,且最少安裝
千元,且最少安裝![]() 臺,最多安裝
臺,最多安裝![]() 臺沖水機,
臺沖水機,
①安裝![]() 臺沖水機每期獲得總利潤
臺沖水機每期獲得總利潤![]() 千元;
千元;
②安裝![]() 臺沖水機的情形:
臺沖水機的情形:
當![]() 時,只有
時,只有![]() 臺沖水機運行,每期總利潤
臺沖水機運行,每期總利潤![]() 千元,且
千元,且![]() ,
,
當![]() 時,有
時,有![]() 臺沖水機運行,每期總利潤
臺沖水機運行,每期總利潤![]() 千元,且
千元,且![]() ,
,
所以![]() (千元);
(千元);
③安裝![]() 臺沖水機的情形:
臺沖水機的情形:
當![]() 時,只有
時,只有![]() 臺沖水機運行,每期總利潤
臺沖水機運行,每期總利潤![]() 千元,且
千元,且![]() ,
,
當![]() 時,有
時,有![]() 臺沖水機運行,每期總利潤
臺沖水機運行,每期總利潤![]() 千元,且
千元,且![]() ,
,
當![]() 時,有
時,有![]() 臺沖水機運行,每期總利潤
臺沖水機運行,每期總利潤![]() 千元,且
千元,且![]() ,
,
所以![]() (千元),
(千元),
綜上,養殖戶欲使每期沖水機總利潤的均值達到最大,應該安裝![]() 臺沖水機.
臺沖水機.


科目:高中數學 來源: 題型:
【題目】為實現有效利用扶貧資金,增加貧困村民的收入,扶貧工作組結合某貧困村水質優良的特點,決定利用扶貧資金從外地購買甲、乙、丙三種魚苗在魚塘中進行養殖試驗,試驗后選擇其中一種進行大面積養殖,已知魚苗甲的自然成活率為0.8.魚苗乙,丙的自然成活率均為0.9,且甲、乙、丙三種魚苗是否成活相互獨立.
(1)試驗時從甲、乙,丙三種魚苗中各取一尾,記自然成活的尾數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)試驗后發現乙種魚苗較好,扶貧工作組決定購買![]() 尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
尾乙種魚苗進行大面積養殖,為提高魚苗的成活率,工作組采取增氧措施,該措施實施對能夠自然成活的魚苗不產生影響.使不能自然成活的魚苗的成活率提高了50%.若每尾乙種魚苗最終成活后可獲利10元,不成活則虧損2元,且扶貧工作組的扶貧目標是獲利不低于37.6萬元,問需至少購買多少尾乙種魚苗?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某房產中介統計了深圳市某高檔小區從2018年12月至2019年11月當月在售二手房均價(單位:萬元/平方米)的散點圖,如下圖所示,圖中月份代碼1至12分別對應2018年12月至2019年11月的相應月份.
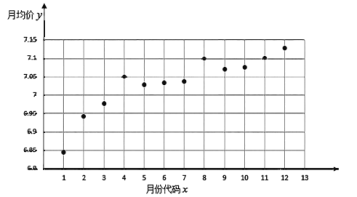
根據散點圖選擇![]() 和
和![]() 兩個模型進行擬合,根據數據處理得到兩個回歸方程分別為
兩個模型進行擬合,根據數據處理得到兩個回歸方程分別為![]() 和
和![]() ,并得到以下一些統計量的值:
,并得到以下一些統計量的值:
|
| |
殘差平方和 | 0.0148557 | 0.0048781 |
總偏差平方和 | 0.069193 | |
(1)請利用相關指數![]() 判斷哪個模型的擬合效果更好;
判斷哪個模型的擬合效果更好;
(2)某位購房者擬于2020年5月份購買深圳市福田區![]() 平方米的二手房(欲購房為其家庭首套房).若該小區所有住房的房產證均已滿3年,請你利用(1)中擬合效果更好的模型解決以下問題:
平方米的二手房(欲購房為其家庭首套房).若該小區所有住房的房產證均已滿3年,請你利用(1)中擬合效果更好的模型解決以下問題:
(i)估算該購房者應支付的購房金額.(購房金額=房款+稅費;房屋均價精確到0.01萬元/平方米)
(ii)若該購房者擬用不超過760萬元的資金購買該小區一套二手房,試估算其可購買的最大面積(精確到1平方米)
附注:根據有關規定,二手房交易需要繳納若干項稅費,稅費是按照房屋的計稅價格進行征收.(計稅價格=房款)
征收方式見下表:
購買首套房面積 |
|
|
|
契稅(買方繳納)的稅率 |
|
|
|
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關指數 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某快餐連鎖店招聘外賣騎手,該快餐連鎖店提供了兩種日工資方案:方案①:規定每日底薪50元,快遞業務每完成一單提成3元;方案②:規定每日底薪100元,快遞業務的前44單沒有提成,從第45單開始,每完成一單提成5元.該快餐連鎖店記錄了每天騎手的人均業務量.現隨機抽取100天的數據,將樣本數據分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七組,整理得到如圖所示的頻率分布直方圖.
七組,整理得到如圖所示的頻率分布直方圖.
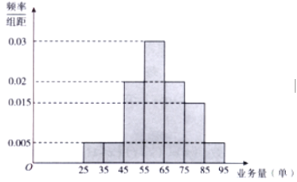
(1)隨機選取一天,估計這一天該連鎖店的騎手的人均日快遞業務量不少于65單的概率;
(2)若騎手甲、乙選擇了日工資方案①,丙、丁選擇了日工資方案②.現從上述4名騎手中隨機選取2人,求至少有1名騎手選擇方案①的概率;
(3)若從人均日收入的角度考慮,請你利用所學的統計學知識為新聘騎手做出日工資方案的選擇,并說明理由.(同組中的每個數據用該組區間的中點值代替)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xoy中,以坐標原點O為極點,x軸正半軸為極軸建立極坐標系。已知曲線C的極坐標方程為![]() ,過點
,過點![]() 的直線l的參數方程為
的直線l的參數方程為 (為參數),直線l與曲線C交于M、N兩點。
(為參數),直線l與曲線C交于M、N兩點。
(1)寫出直線l的普通方程和曲線C的直角坐標方程:
(2)若![]() 成等比數列,求a的值。
成等比數列,求a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,若存在正常數
,若存在正常數![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 成立,我們稱函數
成立,我們稱函數![]() 為“
為“![]() 同比不減函數”.
同比不減函數”.
(1)求證:對任意正常數![]() ,
,![]() 都不是“
都不是“![]() 同比不減函數”;
同比不減函數”;
(2)若函數![]() 是“
是“![]() 同比不減函數”,求
同比不減函數”,求![]() 的取值范圍;
的取值范圍;
(3)是否存在正常數![]() ,使得函數
,使得函數![]() 為“
為“![]() 同比不減函數”,若存在,求
同比不減函數”,若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次期末數學測試中,唐老師任教班級學生的考試得分情況如表所示:
分數區間 |
|
|
|
|
|
人數 | 2 | 8 | 32 | 38 | 20 |
(1)根據上述表格,試估計唐老師所任教班級的學生在本次期末數學測試的平均成績;
(2)現從成績在![]() 中按照分數段,采取分層抽樣的方法隨機抽取5人,再在這5人中隨機抽取2人作小題得分分析,求恰有1人的成績在
中按照分數段,采取分層抽樣的方法隨機抽取5人,再在這5人中隨機抽取2人作小題得分分析,求恰有1人的成績在![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com