
| A. | (-∞,0) | B. | (0,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | $({\frac{1}{e},+∞})$ |
分析 令2017g(x)=$\frac{f(x)}{{e}^{x}}$,(x∈R),從而求導g′(x)<0,從而可判斷y=g(x)單調(diào)遞減,從而可得到不等式的解集.
解答 解:設2017g(x)=$\frac{f(x)}{{e}^{x}}$,由f(x)>f′(x),
得:g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$<0,
故函數(shù)g(x)在R遞減,
由f(x)+2017為奇函數(shù),得f(0)=-2017,
∴g(0)=-1,
∵f(x)+2017ex<0,∴$\frac{f(x)}{{e}^{x}}$<-2017,即g(x)<g(0),
結合函數(shù)的單調(diào)性得:x>0,
故不等式f(x)+2017ex<0的解集是(0,+∞).
故選B.
點評 本題考查了導數(shù)的綜合應用及函數(shù)的性質(zhì)的應用,構造函數(shù)的思想,閱讀分析問題的能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:填空題
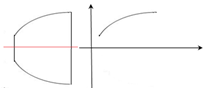 學完解析幾何和立體幾何后,某同學發(fā)現(xiàn)自己家碗的側(cè)面可以看做拋物線的一部分曲線圍繞其對稱軸旋轉(zhuǎn)而成,他很想知道拋物線的方程,決定把拋物線的頂點確定為原點,對稱軸確定為x軸,建立如圖所示的平面直角坐標系,但是他無法確定碗底中心到原點的距離,請你通過對碗的相關數(shù)據(jù)的測量以及進一步的計算,幫助他求出拋物線的方程.你需要測量的數(shù)據(jù)是碗底的直徑2m,碗口的直徑2n,碗的高度h(所有測量數(shù)據(jù)用小寫英文字母表示),算出的拋物線標準方程為y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.
學完解析幾何和立體幾何后,某同學發(fā)現(xiàn)自己家碗的側(cè)面可以看做拋物線的一部分曲線圍繞其對稱軸旋轉(zhuǎn)而成,他很想知道拋物線的方程,決定把拋物線的頂點確定為原點,對稱軸確定為x軸,建立如圖所示的平面直角坐標系,但是他無法確定碗底中心到原點的距離,請你通過對碗的相關數(shù)據(jù)的測量以及進一步的計算,幫助他求出拋物線的方程.你需要測量的數(shù)據(jù)是碗底的直徑2m,碗口的直徑2n,碗的高度h(所有測量數(shù)據(jù)用小寫英文字母表示),算出的拋物線標準方程為y2=$\frac{{n}^{2}-{m}^{2}}{h}$x.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
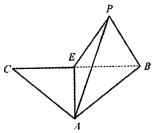 等腰三角形ABC,E為底邊BC的中點,沿AE折疊,如圖,將C折到點P的位置,使P-AE-C為120°,設點P在面ABE上的射影為H.
等腰三角形ABC,E為底邊BC的中點,沿AE折疊,如圖,將C折到點P的位置,使P-AE-C為120°,設點P在面ABE上的射影為H.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | {0} | B. | {2} | C. | {2,4} | D. | {0,1,2} |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:選擇題
| A. | $\frac{1}{16}$ | B. | $\frac{{\root{3}{4}}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\root{3}{4}}}{8}$ |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
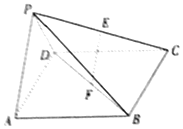 在四棱錐中P-ABCD,底面ABCD是正方形,側(cè)面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分別為PC、BD的中點.
在四棱錐中P-ABCD,底面ABCD是正方形,側(cè)面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD、E、F,分別為PC、BD的中點.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:填空題
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
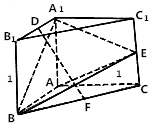 已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四邊形A1ACC1和四邊形A1ABB1均為正方形,D,E,F(xiàn)分別是A1B1,C1C,BC的中點,AB=1.
已知三棱柱ABC-A1B1C1中,底面三角形ABC是直角三角形,四邊形A1ACC1和四邊形A1ABB1均為正方形,D,E,F(xiàn)分別是A1B1,C1C,BC的中點,AB=1.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com