Question

（四川卷理19）如，平面平面，

四邊形與都是直角梯形，

，

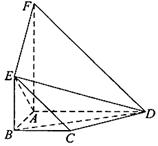
（Ⅰ）證明：四點共面；

（Ⅱ）設(shè)，求二面角的大小；

Answer 1

【解1】：（Ⅰ）延長交的延長線于點，由得

        

延長交的延長線于

同理可得 

故，即與重合

因此直線相交于點，即四點共面。

（Ⅱ）設(shè)，則，

取中點，則，又由已知得，平面

故，與平面內(nèi)兩相交直線都垂直。

所以平面，作，垂足為，連結(jié)

由三垂線定理知為二面角的平面角。

　　　

故所以二面角的大小

【解2】：由平面平面，，得平面，以為坐標原點，射線為軸正半軸，建立如圖所示的直角坐標系

（Ⅰ）設(shè)，則

　　

故，從而由點，得

故四點共面

（Ⅱ）設(shè)，則，

在上取點，使，則

從而

又

在上取點，使，則

從而

故與的夾角等于二面角的平面角，　　，所以二面角的大小

【點評】：此題重點考察立體幾何中四點共面問題和求二面角的問題，考察空間想象能力，幾何邏輯推理能力，以及計算能力；

【突破】：熟悉幾何公理化體系，準確推理，注意書寫格式是順利進行解法1的關(guān)鍵；在解法2中，準確的建系，確定點坐標，熟悉向量的坐標表示，熟悉空間向量的計算在幾何位置的證明，在有關(guān)線段，角的計算中的計算方法是解題的關(guān)鍵。