
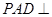 平面
平面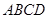 ,
,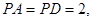 矩形
矩形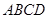 的邊長
的邊長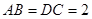 ,
,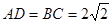 .
.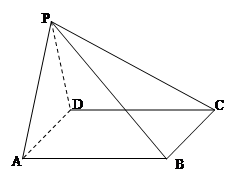
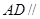 平面
平面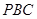 ;
;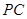 和底面
和底面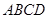 所成角的大小.
所成角的大小.科目:高中數(shù)學 來源:不詳 題型:解答題
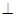 底面ABCD,
底面ABCD,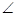 DAB為直角,AB‖CD,AD=CD=2AB,E、F分別為PC、CD的中點.
DAB為直角,AB‖CD,AD=CD=2AB,E、F分別為PC、CD的中點.
 平面BEF;
平面BEF;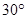 ,求k的取值范圍.
,求k的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
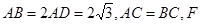 在線段
在線段 上,且
上,且 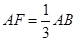 ,將圓沿直徑AB折起,使點C在平面ABD的射影E在BD上.
,將圓沿直徑AB折起,使點C在平面ABD的射影E在BD上.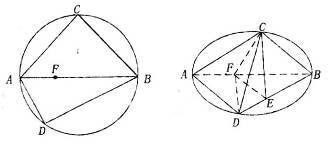
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 為正方形,
為正方形,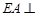 平面
平面 ,
,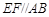 ,
,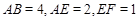 .
.
 在線段
在線段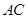 上,且滿足
上,且滿足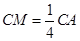 ,求證:
,求證: 平面
平面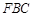 ;
;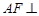 平面
平面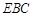 ;
; 的余弦值.
的余弦值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
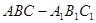 中,
中, ⊥面
⊥面 ,
,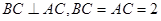 ,
, ,
,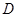 為
為 的中點.
的中點. ;
;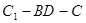 的余弦值;
的余弦值; 上是否存在點
上是否存在點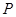 ,使得
,使得 ?請證明你的結(jié)論.
?請證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
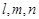 表示不同的直線,
表示不同的直線,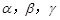 表示不同的平面,給出下列四個命題:
表示不同的平面,給出下列四個命題: 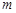 ∥
∥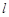 ,且
,且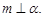 則
則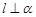 ;
; 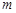 ∥
∥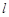 ,且
,且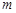 ∥
∥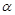 .則
.則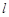 ∥
∥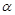 ;
;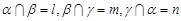 ,則
,則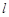 ∥m∥n;
∥m∥n; 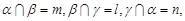 且n∥
且n∥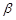 ,則
,則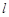 ∥m.
∥m.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題

| A.AC⊥BD |
| B.AC∥截面PQMN |
| C.AC=BD |
| D.異面直線PM與BD所成的角為45° |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com