



科目:高中數學 來源: 題型:
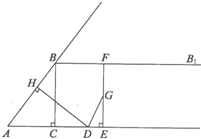 如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,過點B作射線BBl∥AC.動點D從點A出發沿射線AC方向以每秒5個單位的速度運動,同時動點E從點C出發沿射線AC方向以每秒3個單位的速度運動.過點D作DH⊥AB于H,過點E作EF⊥AC交射線BB1于F,G是EF中點,連接DG.設點D運動的時間為t秒.
如圖,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,過點B作射線BBl∥AC.動點D從點A出發沿射線AC方向以每秒5個單位的速度運動,同時動點E從點C出發沿射線AC方向以每秒3個單位的速度運動.過點D作DH⊥AB于H,過點E作EF⊥AC交射線BB1于F,G是EF中點,連接DG.設點D運動的時間為t秒.| 3 | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•青島二模)如圖,在多面體ABC-A1B1C1中,四邊形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青島二模)如圖,在多面體ABC-A1B1C1中,四邊形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=| 1 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com