
若函數f(x)=x+x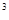 , x
, x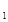 ,x
,x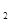
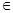 R,且x
R,且x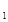 +x
+x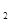 >0,則f(x
>0,則f(x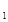 )+f(x
)+f(x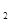 )的值
)的值
A、一定大于0 B、一定小于0 C、一定等于0 D、正負都有可能
科目:高中數學 來源: 題型:單選題
若函數 f(x)=ax (a>0,a≠1 ) 的部分對應值如表:
則不等 式f-1(│x│<0)的解集是
查看答案和解析>>
科目:高中數學 來源:2014屆江西贛州會昌中學高二下學期第一次月考理科數學試卷(解析版) 題型:填空題
對于三次函數f(x)=ax3+bx2+cx+d(a≠0),定義:設f″(x)是函數y=f(x)的導數y=f′(x)的導數,若方程f″(x)=0有實數解x0,則稱點 為函數y=f(x)的“拐點”.有同學發現“任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心;且“拐點”就是對稱中心.”請你根據這一發現,請回答問題:
為函數y=f(x)的“拐點”.有同學發現“任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心;且“拐點”就是對稱中心.”請你根據這一發現,請回答問題:
若函數 ,
,
則 = .
= .
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省青州市高三2月月考理科數學 題型:填空題
給出下列六個命題:
①函數f(x)=lnx-2+x在區間(1 , e)上存在零點;
②若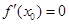 ,則函數y=f(x)在x=x0處取得極值;
,則函數y=f(x)在x=x0處取得極值;
③若m≥-1,則函數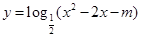 的值域為R;
的值域為R;
④“a=1”是“函數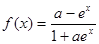 在定義域上是奇函數”的充分不必要條件。
在定義域上是奇函數”的充分不必要條件。
⑤函數y=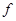 (1+x)的圖像與函數y=f(l-x)的圖像關于y軸對稱;
(1+x)的圖像與函數y=f(l-x)的圖像關于y軸對稱;
⑥滿足條件AC=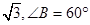 ,AB =1的三角形△ABC有兩個.
,AB =1的三角形△ABC有兩個.
其中正確命題的個數是 。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知4個命題:
①若等差數列{![]() }的前n項和為
}的前n項和為![]() ,則三點(10,
,則三點(10,![]() ),(100,
),(100,![]() ),(110,
),(110,![]() )共線;
)共線;
②命題“![]() ∈R,使得
∈R,使得![]() +1>3x”的否定是“
+1>3x”的否定是“![]() ∈R,
∈R,![]() +1≤3x”;
+1≤3x”;
③若函數f(x)=x-![]() +k在(0,1)沒有零點,則k的取值范圍是k≥2;
+k在(0,1)沒有零點,則k的取值范圍是k≥2;
③f(x)是定義在R上的奇函數![]() (x)>0,且f(2)=
(x)>0,且f(2)=![]() ,則xf(x)<1的解集為(-2,2).
,則xf(x)<1的解集為(-2,2).
其中正確的是_____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com