Question

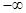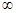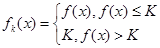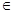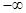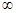設函數在（，+）內有意義.對于給定的正數K，已知函數，取函數=.若對任意的（，+），恒有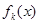=，則K的最小值為            .

Answer 1

2

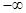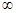解析試題分析：根據新定義的函數建立f_k（x）與f（x）之間的關系，通過二者相等得出實數k滿足的條件，利用導數或者函數函數的單調性求解函數的最值，進而求出k的范圍，進一步得出所要的結果．根據題意，函數在（，+）內有意義.對于給定的正數K，已知函數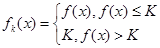，那么可知=，導函數為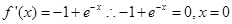 ，當x<0，f’(x)>0;當x>0，f’(x)<0，那么可知函數的單調性為x<0,遞增，x>0，遞減，那么可知在x=0處取得最大值，即為f(0)=3-1=2，那么可知則K的最小值為2，答案為2.
考點：導數求閉區間上函數的最值
點評：本題考查利用導數求閉區間上函數的最值，考查運算求解能力，推理論證能力；考查化歸與轉化思想．對數學思維的要求比較高，有一定的探索性．解題時要認真審題，仔細解答