【題目】在某校冬季長跑活動中,學校要給獲得一二等獎的學生購買獎品,要求花費總額不得超過200元.已知一等獎和二等獎獎品的單架分別為20元10元,一等獎人數與二等獎人數的比值不得高于
,且獲得一等獎的人數不能少于2人,有下列四個結論:①最多可以購買4份一等獎獎品②最多可以購買16份二等獎獎品③購買獎品至少要花費100元④共有20種不同的購買獎品方案其中正確結論的序號為___________.
提分百分百檢測卷單元期末測試卷系列答案
小學期末標準試卷系列答案科目：高中數學 來源： 題型：
【題目】下列命題中正確的個數有（ ）
①向量
與
是共線向量，則A、B、C、D四點必在一直線上；②單位向量都相等；③任一向量與它的相反向量不相等；④共線的向量，若起點不同，則終點一定不同．
A.0B.1C.2D.3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知直線
的參數方程為
（
為參數）.以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的直角坐標方程；
（2）已知點
，直線與曲線交于
兩點，且
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
過點
，順次連接橢圓的四個頂點得到的四邊形的面積為
，點
.
（Ⅰ）求橢圓
的方程.
（Ⅱ）已知點
，是橢圓
上的兩點.
（ⅰ）若
，且
為等邊三角形，求
的面積；
（ⅱ）若
，證明： 
不可能為等邊三角形.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】新型冠狀病毒肺炎疫情爆發以來，疫情防控牽掛著所有人的心. 某市積極響應上級部門的號召，通過沿街電子屏、微信公眾號等各種渠道對此戰“疫”進行了持續、深入的懸窗，幫助全體市民深入了解新冠狀病毒，增強戰勝疫情的信心. 為了檢驗大家對新冠狀病毒及防控知識的了解程度，該市推出了相關的知識問卷，隨機抽取了年齡在15~75歲之間的200人進行調查，并按年齡繪制頻率分布直方圖如圖所示，把年齡落在區間
和
內的人分別稱為“青少年人”和“中老年人”. 經統計“青少年人”和“中老年人”的人數比為19:21. 其中“青少年人”中有40人對防控的相關知識了解全面，“中老年人”中對防控的相關知識了解全面和不夠全面的人數之比是2:1.
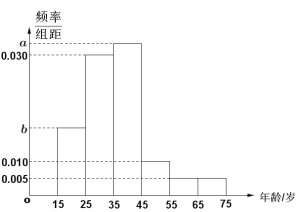
（1）求圖中
的值；
（2）現采取分層抽樣在
和
中隨機抽取8名市民，從8人中任選2人，求2人中至少有1人是“中老年人”的概率是多少？
（3）根據已知條件，完成下面的2×2列聯表，并根據統計結果判斷：能夠有99.9%的把握認為“中老年人”比“青少年人”更加了解防控的相關知識？
了解全面 | 了解不全面 | 合計 | |
青少年人 | |||
中老年人 | |||
合計 |
附表及公式：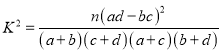
，其中
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線C：
=2px經過點
（1，2）．過點Q（0，1）的直線l與拋物線C有兩個不同的交點A，B，且直線PA交y軸于M，直線PB交y軸于N．
（Ⅰ）求直線l的斜率的取值范圍；
（Ⅱ）設O為原點，
，
，求證：
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用水清洗一堆蔬菜上殘留的農藥，對用一定量的水清洗一次的效果作如下假定：用1個單位量的水可洗掉蔬菜上殘留農藥量的
，用水越多洗掉的農藥量也越多，但總還有農藥殘留在蔬菜上．設用
單位量的水清洗一次以后，蔬菜上殘留的農藥量與本次清洗前殘留的農藥量之比為函數
．
（1）試規定
的值，并解釋其實際意義；
（2）試根據假定寫出函數應該滿足的條件和具有的性質；
（3）設
．現有
單位量的水，可以清洗一次，也可以把水平均分成2份后清洗兩次，試問用哪種方案清洗后蔬菜上殘留的農藥量比較省？說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
