(1)一雙曲線以橢圓16x2+25y2=400的焦點為頂點,橢圓的長軸端點為焦點,求雙曲線的方程.
(2)若拋物線y2=2px(p>0)上一點A到準線及對稱軸的距離分別為10和6,求A點的橫坐標及拋物線的方程.
解:(1)∵橢圓16x
2+25y
2=400的標準形式為

∴橢圓的左右頂點坐標為(5,0)和(-5,0)
∵橢圓的半焦距c=

=3,
∴橢圓的焦點坐標為(3,0)和(-3,0)
∵雙曲線的焦點是橢圓和左右頂點,頂點是橢圓的左右焦點
∴雙曲線的b
2=25-9=16,可得雙曲線的方程是:

-

=1;
(2)∵拋物線y
2=2px(p>0)上一點A到對稱軸的距離為6,
∴設A(x
0,y
0),y
02=2px
0且|y
0|=6,可得2px
0=36…(*)
∵點A到準線的距離為10,
∴x
0+

=10,與(*)聯解,可得
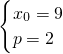
或
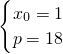
由此可得A點的橫坐標為9,拋物線的方程是y
2=4x;或A點的橫坐標為1,拋物線的方程是y
2=36x.
分析:(1)根據橢圓的基本概念,不難得到雙曲線的頂點坐標和焦點坐標,再利用平方關系算出b的平方,即可得到所求雙曲線的方程.
(2)設A(x
0,y
0),由拋物線上點A到對稱軸的距離為6,得|y
0|=6.由此結合拋物線的標準方程和定義,建立x
0和p的方程組,解之即可得到A點的橫坐標及拋物線的方程.
點評:本題第1問考查了橢圓、雙曲線的標準方程與簡單幾何性質的知識;第2問考查了拋物線的定義與簡單幾何性質,兩題都屬于基礎題.


 =3,
=3, -
- =1;
=1;  =10,與(*)聯解,可得
=10,與(*)聯解,可得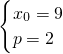 或
或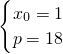


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案