
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (α為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρcosθ=1.
(α為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρcosθ=1.
(1)求C1的極坐標方程,并求C1與C2交點的極坐標![]() ;
;
(2)若曲線C3:θ=β(ρ>0)與C1,C2的交點分別為M,N,求|OM||ON|的值.
【答案】(1)ρ2﹣4ρcosθ=0;C1與C2交點的極坐標為(2,![]() ),(2,
),(2,![]() )(2)4
)(2)4
【解析】
(1)根據同角三角函數關系式,消去參數,可得C1的直角坐標方程,再由x=ρcosθ,y=ρsinθ代入可得極坐標方程;聯立C1與C2的極坐標方程,即可得到交點坐標;
(2)分別聯立曲線C3和C1,C3和C2的極坐標方程,分別得到OM和ON的長度,再求值即可.
解:(1)由![]() (α為參數)消去參數可得(x﹣2)2+y2=4,即x2+y2﹣4x=0,
(α為參數)消去參數可得(x﹣2)2+y2=4,即x2+y2﹣4x=0,
又![]() ,則ρ2﹣4ρcosθ=0,
,則ρ2﹣4ρcosθ=0,
即C1的極坐標方程為ρ=4cosθ.
由![]() ,可得4cos2θ=1,又
,可得4cos2θ=1,又![]() ,所以θ=±
,所以θ=±![]() ,ρ=2.
,ρ=2.
即C1與C2交點的極坐標為(2,![]() ),(2,
),(2,![]() ).
).
(2)由![]() ,可得|OM|=4cosβ,
,可得|OM|=4cosβ,
由![]() ,可得|ON|
,可得|ON|![]() ,
,
所以|OM||ON|=4.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:高中數學 來源: 題型:
【題目】在四邊形ABCD中,BD為四邊形的一條對角線,且![]() ,將
,將![]() 沿BD向上翻折,當點A在平面BCD內的投影恰好為
沿BD向上翻折,當點A在平面BCD內的投影恰好為![]() 的外心E時,設直線AE與平面ABC,ACD,ABD的夾角分別為
的外心E時,設直線AE與平面ABC,ACD,ABD的夾角分別為![]() ,
,![]() ,
,![]() ,則( )
,則( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以坐標原點O為極點,以x軸正半軸為極軸,建立極坐標系,曲線C的極坐標方程為![]() 射線
射線![]() 交曲線C于點A,傾斜角為α的直線l過線段OA的中點B且與曲線C交于P、Q兩點.
交曲線C于點A,傾斜角為α的直線l過線段OA的中點B且與曲線C交于P、Q兩點.
(1)求曲線C的直角坐標方程及直線l的參數方程;
(2)當直線l傾斜角α為何值時, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,四邊形ABCD為等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E為AB的中點,連接DE,DB(如圖2).
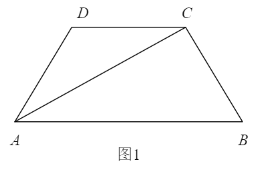
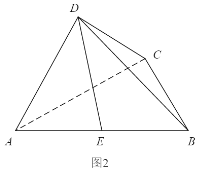
(1)求證:BC⊥AD
(2)求直線DE與平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,曲線
,曲線![]() 上任意一點到
上任意一點到![]() 的距離等于該點到直線
的距離等于該點到直線![]() 的距離.
的距離.
(Ⅰ)求![]() 及曲線
及曲線![]() 的方程;
的方程;
(Ⅱ)若直線![]() 與橢圓只有一個交點
與橢圓只有一個交點![]() ,與曲線
,與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“珠算之父”程大位是我國明代著名的數學家,他的應用巨著《算法統綜》中有一首“竹筒容米”問題:“家有九節竹一莖,為因盛米不均平,下頭三節四升五,上梢四節三升八,唯有中間兩節竹,要將米數次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容積依次相差同一數量.)用你所學的數學知識求得中間兩節竹的容積為
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() .過焦點且垂直于
.過焦點且垂直于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 相交所得的弦長為3,直線
相交所得的弦長為3,直線![]() 與橢圓
與橢圓![]() 相切.
相切.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,若
兩點,若![]() ,問直線
,問直線![]() 是否存在?若存在,求直線
是否存在?若存在,求直線![]() 的斜率
的斜率![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】口袋中有大小、形狀、質地相同的兩個白球和三個黑球.現有一抽獎游戲規則如下:抽獎者每次有放回的從口袋中隨機取出一個球,最多取球2n+1(n![]() )次.若取出白球的累計次數達到n+1時,則終止取球且獲獎,其它情況均不獲獎.記獲獎概率為
)次.若取出白球的累計次數達到n+1時,則終止取球且獲獎,其它情況均不獲獎.記獲獎概率為![]() .
.
(1)求![]() ;
;
(2)證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系.每年交強險最終保險費計算方法是:交強險最終保險費![]() ,其中a為交強險基礎保險費,A為與道路交通事故相聯系的浮動比率,同時滿足多個浮動因素的,按照向上浮動或者向下浮動比率的高者計算.按照我國《機動車交通事故責任強制保險基礎費率表》的規定:普通6座以下私家車的交強險基礎保險費
,其中a為交強險基礎保險費,A為與道路交通事故相聯系的浮動比率,同時滿足多個浮動因素的,按照向上浮動或者向下浮動比率的高者計算.按照我國《機動車交通事故責任強制保險基礎費率表》的規定:普通6座以下私家車的交強險基礎保險費![]() 為950元,交強險費率浮動因素及比率如下表:
為950元,交強險費率浮動因素及比率如下表:
交強險浮動因素和浮動費率比率表 | ||
類型 | 浮動因素 | 浮動比率 |
| 上一個年度未發生有責任道路交通事故 |
|
| 上兩個年度未發生有責任道路交通事故 |
|
| 上三個及以上年度未發生有責任道路交通事故 |
|
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 |
|
| 上一個年度發生兩次及以上有責任道路交通事故 |
|
| 上一個年度發生有責任道路交通死亡事故 |
|
某機構為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了100輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計結果如下表:
類型 |
|
|
|
|
|
|
數量 | 25 | 10 | 10 | 25 | 20 | 10 |
以這100輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題.
(1)記X為一輛該品牌車在第四年續保時的費用,求X的分布列與數學期望(數學期望值保留到個位數字);
(2)某二手車銷售商專門銷售這一品牌的二手車,且將經銷商購車后下一年的交強險最終保險費高于交強險基礎保險費![]() 的車輛記為事故車,假設購進一輛事故車虧損3000元,購進一輛非事故車盈利5000元.
的車輛記為事故車,假設購進一輛事故車虧損3000元,購進一輛非事故車盈利5000元.
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至少有一輛是事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com