
【題目】已知各項均為整數的數列{an}滿足an2≤1,1≤a12+a22+…+an2≤m,m,n∈N* .
(1)若m=1,n=2,寫出所有滿足條件的數列{an};
(2)設滿足條件的{an}的個數為f(n,m).
①求f(2,2)和f(2016,2016);
②若f(m+1,m)>2016,試求m的最小值.
【答案】
(1)解:當m=1,n=2時,1≤ ![]() ≤1,又
≤1,又 ![]() ≤1
≤1
∴{an}為0,1或0,﹣1或1,0或﹣1,0
(2)解:①當m=n=2時,1≤ ![]() ≤2,a1、a2取值共有:32﹣1=8種,
≤2,a1、a2取值共有:32﹣1=8種,
即f(2,2)=8,
又當m=n=2016時,1≤ ![]() ≤2016,a1、a2、a2016取值共有:32016﹣1種;
≤2016,a1、a2、a2016取值共有:32016﹣1種;
即f(2016,2016)=32016﹣1f(m+1,m)>2016即1≤ ![]() ≤m
≤m
②數列{an}需滿足不能全為0,不能沒有0(即每項均為1或﹣1),
∴f(m+1,m)=3m+1﹣1﹣2m+1,
即考慮3m+1﹣2m+1﹣1>2016,
令g(m)=3m+1﹣2m+1,
則g(m+1)﹣g(m)=2×3m+1﹣2m+1>0
∴g(m)單調增
又g(6)=2059成立,
∴m最小值為6
【解析】(1)若m=1,n=2,1≤ ![]() ≤1,又
≤1,又 ![]() ≤1,即可求得所有滿足條件的數列{an};(2)①)當m=n=2時,1≤
≤1,即可求得所有滿足條件的數列{an};(2)①)當m=n=2時,1≤ ![]() ≤2,由a1、a2可能取值為0,1,﹣1,則a1、a2取值共有:32﹣1=8種,當m=n=2016時,1≤
≤2,由a1、a2可能取值為0,1,﹣1,則a1、a2取值共有:32﹣1=8種,當m=n=2016時,1≤ ![]() ≤2016,a1、a2、a2016可能取值為0,1,﹣1,共有:32016﹣1種;②由f(m+1,m)=3m+1﹣1﹣2m+1 , 將原式轉換為3m+1﹣2m+1>2017,構造輔助函數g(m)=3m+1﹣2m+1 , 做差g(m+1)﹣g(m)=2×3m+1﹣2m+1>0,g(x)單調遞增,又g(6)=2059成立,即可求得m的最小值.
≤2016,a1、a2、a2016可能取值為0,1,﹣1,共有:32016﹣1種;②由f(m+1,m)=3m+1﹣1﹣2m+1 , 將原式轉換為3m+1﹣2m+1>2017,構造輔助函數g(m)=3m+1﹣2m+1 , 做差g(m+1)﹣g(m)=2×3m+1﹣2m+1>0,g(x)單調遞增,又g(6)=2059成立,即可求得m的最小值.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】觀察下列等式
l+2+3+…+n= ![]() n(n+l);
n(n+l);
l+3+6+…+ ![]() n(n+1)=
n(n+1)= ![]() n(n+1)(n+2);
n(n+1)(n+2);
1+4+10+… ![]() n(n+1)(n+2)=
n(n+1)(n+2)= ![]() n(n+1)(n+2)(n+3);
n(n+1)(n+2)(n+3);
可以推測,1+5+15+…+ ![]() n(n+1)(n+2)(n+3)= .
n(n+1)(n+2)(n+3)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0且a≠1,函數 ![]() ,
,
(1)求函數f(x)的定義域;
(2)將函數y=f(x)的圖象向右平移兩個單位后得到函數y=g(x)的圖象,若實數x滿足g(x)≥0,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
, ![]() .
.
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)討論![]() 在區間
在區間![]() 上的極值點個數;
上的極值點個數;
(3)是否存在![]() ,使得
,使得![]() 在區間
在區間![]() 上與
上與![]() 軸相切?若存在,求出所有
軸相切?若存在,求出所有![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC= ![]() ,AB=1,BD=PA=2,M 為PD的中點.
,AB=1,BD=PA=2,M 為PD的中點. 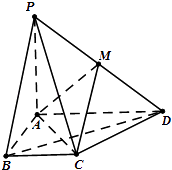
(1)求異面直線BD與PC所成角的余弦值;
(2)求二面角A﹣MC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
男 | 女 | 總計 | |
需要幫助 | 40 | m | 70 |
不需要幫助 | n | 270 | s |
總計 | 200 | t | 500 |
(1)求m,n,s,t的值;
(2)估計該地區老年人中,需要志愿者提供幫助的比例;
(3)能否有99%的把握認為該地區的老年人是否需要志愿者幫助與性別有關.
參考公式:
隨機變量K2= ![]() ,n=a+b+c+d
,n=a+b+c+d
在2×2列聯表:
y1 | y2 | 總計 | |
x1 | a | b | a+b |
x2 | c | d | c+d |
總計 | a+c | b+d | a+b+c+d |
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com