
在數列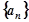 中,已知
中,已知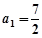 ,
,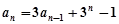 (
(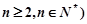 .
.
(1)求證: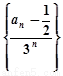 是等差數列;
是等差數列;
(2)求數列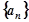 的通項公式
的通項公式 及它的前
及它的前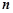 項和
項和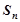 .
.
(1)見解析(2)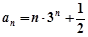 ,
,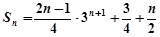
【解析】本試題主要是考查了等差數列的定義以及錯位相減法的求和的綜合運用。
(1)根據已知的遞推關系式,得到數列的相鄰兩項的關系式,進而結合定義證明。
(2)在第一問的基礎上,得到數列的通項公式,然后借助于錯位相減法得到結論。
(1)證明:∵ 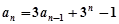 (
(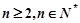 )
)
∴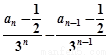
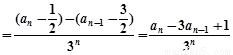
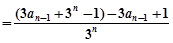
 為常數
為常數
∴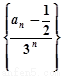 是等差數列,且公差為1.
…………………… 5分
是等差數列,且公差為1.
…………………… 5分
(2)解:由(1)知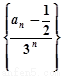 是等差數列,且公差為1,且
是等差數列,且公差為1,且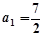
∴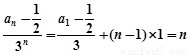 ∴
∴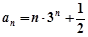 …………… 8分
…………… 8分
∴  ……………
9分
……………
9分
令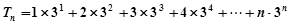 …………①
…………①
則 ……②…………… 10分
……②…………… 10分
兩式相減得:
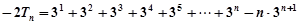 ……………… 11分
……………… 11分

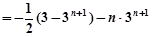 …………… 12分
…………… 12分
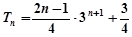 ………………… 13分
………………… 13分
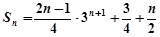 ………………… 14分
………………… 14分


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:高中數學 來源:2010-2011年四川省成都市玉林中學高一下學期期中考試數學 題型:解答題
((本小題滿分14分)
A組.設 是等差數列,
是等差數列, 是各項都為正數的等比數列,且
是各項都為正數的等比數列,且 .
.
(1)求數列 、
、 的通項公式.
的通項公式.
(2)求數列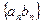 的前
的前 項和
項和
B組.在數列 中,已知:
中,已知: .
.
(1)求證:數列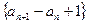 是
是 等比數列.
等比數列.
(2)求數列 的通項公式.
的通項公式.
(3)求和: .
.
查看答案和解析>>
科目:高中數學 來源:2011屆河北省唐山一中高三高考仿真理數 題型:解答題
(本小題滿分12分)
在數列 中,已知
中,已知 且
且 。
。
(1)記 證明:數列
證明:數列 是等差數列,并求數列
是等差數列,并求數列 的通項公式;
的通項公式;
(2)設 求
求 的值。
的值。
查看答案和解析>>
科目:高中數學 來源:2014屆安徽省六校教育研究會高三素質測試文科數學試卷(解析版) 題型:解答題
在數列 中,已知
中,已知 ,
, .
.
(1)求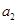 、
、 并判斷
并判斷 能否為等差或等比數列;
能否為等差或等比數列;
(2)令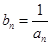 ,求證:
,求證: 為等比數列;
為等比數列;
(3)求數列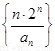 的前n項和
的前n項和 .
.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省紅色六校高三第二次聯考理科數學試卷 題型:解答題
在數列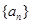 中,已知
中,已知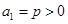 ,且
,且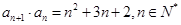 .
.
(1)若數列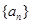 為等差數列,求p的值;
為等差數列,求p的值;
(2)求數列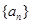 的通項公式;
的通項公式;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com