
【題目】函數![]() ,
,![]() ,其中常數
,其中常數![]() .
.
(1)若函數![]() 與
與![]() 有相同的極值點,求
有相同的極值點,求![]() 的值;
的值;
(2)若![]() ,判斷函數
,判斷函數![]() 與
與![]() 圖象的交點個數.
圖象的交點個數.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,有1個交點;當
時,有1個交點;當![]() 時,有3個交點.
時,有3個交點.
【解析】
(1)先求出![]() 的極值點,再通過
的極值點,再通過![]() 與
與![]() 有相同的極值點,可求出
有相同的極值點,可求出![]() 的值;
的值;
(2)判斷函數![]() 與
與![]() 圖象的交點個數,構造新函數
圖象的交點個數,構造新函數![]() ,可將問題轉化為求函數
,可將問題轉化為求函數![]() 的零點個數,結合a的范圍,利用函數的單調性及函數的性質可判斷函數的零點存在情況.
的零點個數,結合a的范圍,利用函數的單調性及函數的性質可判斷函數的零點存在情況.
解:(1)![]() ,
,![]() 的定義域都為
的定義域都為![]() ,
,
![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
所以函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 處取得極小值;
處取得極小值;
又![]() .
.
∴![]() ,解得
,解得![]() ,
,
經檢驗,滿足題意,故![]() .
.
(2)函數![]() 與
與![]() 的圖象的交點個數等價于函數
的圖象的交點個數等價于函數![]() 的零點個數.
的零點個數.
![]() ,則
,則![]() .
.
①當![]() 時,令
時,令![]() ,則
,則![]() .
.
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
故函數![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
故![]() .
.
則![]() .故
.故![]() 在
在![]() 上是增函數,此時由
上是增函數,此時由![]() ,可得函數
,可得函數![]() 有唯一的零點.
有唯一的零點.
即函數![]() 與
與![]() 的圖象有1個交點;
的圖象有1個交點;
②當![]() 時,
時,![]() ,
,
并且對于負數![]() ,有
,有
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又因為![]() ,
,
所以![]() ,
,
所以![]() .
.
所以在區間![]() 上存在負數
上存在負數![]() ,使得
,使得![]() ,
,
則在![]() 上,
上,![]() ,
,![]() 是增函數,
是增函數,
在區間![]() 上,
上,![]() ,
,![]() 是減函數.
是減函數.
則![]() ,
,![]() .
.
所以在![]() 上,
上,![]() 有且僅有1個零點;
有且僅有1個零點;
在區間![]() 上,
上,![]() ,
,![]() 且
且![]() 是增函數,
是增函數,
所以存在正數![]() ,使得在
,使得在![]() 上,
上,![]() ,
,![]() 是減函數;
是減函數;
在![]() 上,
上,![]() ,
,![]() 是增函數.
是增函數.
于是有![]() ,
,![]() .
.
所以在![]() 上,
上,![]() 恰有唯一的零點
恰有唯一的零點
所以當![]() 時,
時,![]() 在
在![]() 上恰有三個不同的零點.
上恰有三個不同的零點.
即函數![]() 與
與![]() 的圖象有3個交點.
的圖象有3個交點.
綜上所述,當![]() 時,函數
時,函數![]() 與
與![]() 的圖象有1個交點;當
的圖象有1個交點;當![]() 時,函數
時,函數![]() 與
與![]() 的圖象有3個交點.
的圖象有3個交點.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,則下列判斷正確的是( )
,則下列判斷正確的是( )
A.函數![]() 的最小正周期為
的最小正周期為![]() ,在
,在![]() 上單調遞增
上單調遞增
B.函數![]() 的最小正周期為
的最小正周期為![]() ,在
,在![]() 上單調遞增
上單調遞增
C.函數![]() 的最小正周期為
的最小正周期為![]() ,在
,在![]() 上單調遞增
上單調遞增
D.函數![]() 的最小正周期為
的最小正周期為![]() ,在
,在![]() 上單調遞增
上單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,直線l1的參數方程為![]() (t為參數),直線l2的參數方程為
(t為參數),直線l2的參數方程為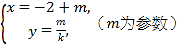 .設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
.設l1與l2的交點為P,當k變化時,P的軌跡為曲線C.
(1)寫出C的普通方程;
(2)以坐標原點為極點,x軸正半軸為極軸建立極坐標系,設l3:ρ(cosθ+sinθ) ![]() =0,M為l3與C的交點,求M的極徑.
=0,M為l3與C的交點,求M的極徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】盲盒里面通常裝的是動漫、影視作品的周邊,或者設計師單獨設計出來的玩偶.由于盒子上沒有標注,購買者只有打開才會知道自己買到了什么,因此這種驚喜吸引了眾多年輕人,形成了“盲盒經濟”.某款盲盒內可能裝有某一套玩偶的![]() 、
、![]() 、
、![]() 三種樣式,且每個盲盒只裝一個.
三種樣式,且每個盲盒只裝一個.
(1)若每個盲盒裝有![]() 、
、![]() 、
、![]() 三種樣式玩偶的概率相同.某同學已經有了
三種樣式玩偶的概率相同.某同學已經有了![]() 樣式的玩偶,若他再購買兩個這款盲盒,恰好能收集齊這三種樣式的概率是多少?
樣式的玩偶,若他再購買兩個這款盲盒,恰好能收集齊這三種樣式的概率是多少?
(2)某銷售網點為調查該款盲盒的受歡迎程度,隨機發放了200份問卷,并全部收回.經統計,有![]() 的人購買了該款盲盒,在這些購買者當中,女生占
的人購買了該款盲盒,在這些購買者當中,女生占![]() ;而在未購買者當中,男生女生各占
;而在未購買者當中,男生女生各占![]() .請根據以上信息填寫下表,并分析是否有
.請根據以上信息填寫下表,并分析是否有![]() 的把握認為購買該款盲盒與性別有關?
的把握認為購買該款盲盒與性別有關?
女生 | 男生 | 總計 | |
購買 | |||
未購買 | |||
總計 |
參考公式: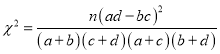 ,其中
,其中![]() .
.
span>參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)該銷售網點已經售賣該款盲盒6周,并記錄了銷售情況,如下表:
周數 | 1 | 2 | 3 | 4 | 5 | 6 |
盒數 | 16 | ______ | 23 | 25 | 26 30 |
由于電腦故障,第二周數據現已丟失,該銷售網點負責人決定用第4、5、6周的數據求線性回歸方程,再用第1、3周數據進行檢驗.
①請用4、5、6周的數據求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(注: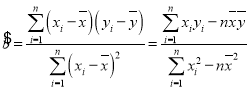 ,
,![]() )
)
②若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2盒,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,一動圓與直線
,一動圓與直線![]() 相切且與圓
相切且與圓![]() 外切.
外切.
(1)求動圓圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)若經過定點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,
兩點, ![]() 是線段
是線段![]() 的中點,過
的中點,過![]() 作
作![]() 軸的平行線與曲線
軸的平行線與曲線![]() 相交于點
相交于點![]() ,試問是否存在直線
,試問是否存在直線![]() ,使得
,使得![]() ,若存在,求出直線
,若存在,求出直線![]() 的方程,若不存在,說明理由.
的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】謝爾賓斯三角形是一種分形,其具體操作是取一個實心的三角形沿三邊中點的連線,將它分成四個小三角形,去掉中間的那一個小三角形,然后對其余三個小三角形重復以上步驟,得到如下的系列圖稱之為謝爾賓斯:三角形.在第五個圖形中,若隨機的投入一個質點,則質點落入“空白”處的概率為( )
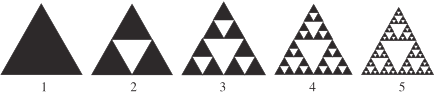
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
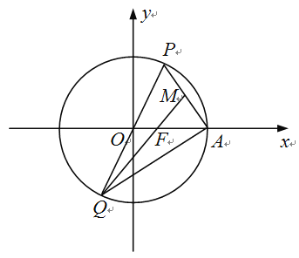
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若
的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若![]() ,
,![]() 的面積是
的面積是![]() 面積的3倍.
面積的3倍.
(1)求橢圓C的標準方程;
(2)已知M為線段PA的中點,連結QA,QM.
①求證:Q,F,M三點共線;
②記直線QP,QM,QA的斜率分別為![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
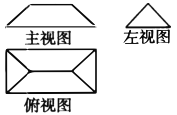
【題目】中國古代數學名著《九章算術》中記載:“芻(chú)甍(méng)者,下有袤有廣,而上有袤無廣.芻,草也.甍,屋蓋也.”翻譯為“底面有長有寬為矩形,頂部只有長沒有寬為一條棱.芻甍字面意思為茅草屋頂.”若芻甍的三視圖如圖所示,主視圖是上底為2,下底為4,高為1的等腰梯形,左視圖是底邊為2的等腰三角形,則該幾何體的體積為( ).
A.![]() B.
B.![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是首項為1的等差數列,數列
是首項為1的等差數列,數列![]() 是公比不為1的等比數列,且滿足
是公比不為1的等比數列,且滿足![]() ,
,![]() ,
,![]()
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)令![]() ,記數列
,記數列![]() 的前n項和為
的前n項和為![]() ,求證:對任意的
,求證:對任意的![]() ,都有
,都有![]() ;
;
(3)若數列![]() 滿足
滿足![]() ,
,![]() ,記
,記![]() ,是否存在整數
,是否存在整數![]() ,使得對任意的
,使得對任意的![]() 都有
都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com