【題目】隨著我國經濟模式的改變，電商已成為當今城鄉種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內，每售出
噸該商品可獲利潤
萬元，未售出的商品，每噸虧損
萬元根據往年的銷售資料，得到該商品一個銷售季度內市場需求量的頻率分布直方圖如圖所示.已知電商為下一個銷售季度籌備了
噸該商品，現以
單位:噸，
)表示下一個銷售季度的市場需求量，
(單位:萬 元)表示該電商下“個銷售季度內經銷該商品獲得的利潤.
（1）視分布在各區間內的頻率為相應的概率，求
；
（2）將表示為的函數，求出該函數表達式；
（3）在頻率分布直方圖的市場需求量分組中，若以市場需求量落入該區間的頻率作為市場需求量的概率，求該季度利潤不超過
萬元的概率.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知線段
上有
個確定的點（包括端點
與
）.現對這些點進行往返標數（從
…進行標數，遇到同方向點不夠數時就“調頭”往回數）.如圖：在點上標
，稱為點，然后從點開始數到第二個數，標上
，稱為點，再從點開始數到第三個數，標上
，稱為點（標上數
的點稱為點），……，這樣一直繼續下去，直到，，，…，
都被標記到點上，則點上的所有標記的數中，最小的是_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區有小學21所，中學14所，現采用分層抽樣的方法從這些學校中抽取5所學校，對學生進行視力檢查．
（1）求應從小學、中學中分別抽取的學校數目；
（2）若從抽取的5所學校中抽取2所學校作進一步數據
①列出所有可能抽取的結果；
②求抽取的2所學校至少有一所中學的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系中，點 P的極坐標是 
，曲線 C的極坐標方程為 
．以極點為坐標原點，極軸為 x軸的正半軸建立平面直角坐標系，斜率為﹣1的直線 l經過點P．
（1）寫出直線 l的參數方程和曲線 C的直角坐標方程；
（2）若直線 l和曲線C相交于兩點A，B，求 
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】正方體ABCD﹣A1B1C1D1的棱長為1，點E，F分別是棱D1C1 ， B1C1的中點，過E，F作一平面α，使得平面α∥平面AB1D1 ， 則平面α截正方體的表面所得平面圖形為（ ）
A.三角形
B.四邊形
C.五邊形
D.六邊形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的最小正周期為
，且直線
是其圖象的一條對稱軸．
（1）求函數
的解析式；
（2）在
中，角
、
、
所對的邊分別為
、
、
，且
，
，若角滿足
，求
的取值范圍；
（3）將函數
的圖象向右平移
個單位，再將所得的圖象上每一點的縱坐標不變，橫坐標伸長為原來的
倍后所得到的圖象對應的函數記作
，已知常數
，
，且函數
在
內恰有
個零點，求常數
與
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市教育部門為了解全市高三學生的身高發育情況，從本市全體高三學生中隨機抽取了100人的身高數據進行統計分析．經數據處理后，得到了如下圖1所示的頻事分布直方圖，并發現這100名學生中，身高不低于1.69米的學生只有16名，其身高莖葉圖如下圖2所示，用樣本的身高頻率估計該市高一學生的身高概率．
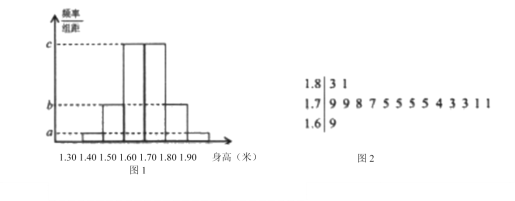
（1）求該市高三學生身高高于1.70米的概率，并求圖1中
、
、
的值．
（2）若從該市高三學生中隨機選取3名學生，記
為身高在
的學生人數，求的分布列和數學期望；
（3）若變量
滿足
且
，則稱變量滿足近似于正態分布
的概率分布．如果該市高三學生的身高滿足近似于正態分布
的概率分布，則認為該市高三學生的身高發育總體是正常的．試判斷該市高三學生的身高發育總體是否正常，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設拋物線C：y2=2px（p＞0）的焦點為F，點M在C上，|MF|=5，若以MF為直徑的圓過點（0，2），則C的方程為（ ）
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
