已知函數f(x)＝loga(x＋1)(a>1)，若函數y＝g(x)的圖象上任意一點P關于原點對稱的點Q的軌跡恰好是函數f(x)的圖象．
(1)寫出函數g(x)的解析式；
(2)當x∈[0,1)時總有f(x)＋g(x)≥m成立，求m的取值范圍．
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝ax2－|x|＋2a－1(a為實常數)．
(1)若a＝1，作函數f(x)的圖象；
(2)設f(x)在區間[1，2]上的最小值為g(a)，求g(a)的表達式；
(3)設h(x)＝
，若函數h(x)在區間[1，2]上是增函數，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝x2＋4ax＋2a＋6.
(1) 若f(x)的值域是[0，＋∞)，求a的值；
(2) 若函數f(x)≥0恒成立，求g(a)＝2－a|a－1|的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)是定義在R上的偶函數，且x≥0時，
.
(1)求f(-1)的值；
(2)求函數f(x)的值域A；
(3)設函數
的定義域為集合B，若AÍB，求實數a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數
的定義域為
.設點P是函數圖象上的任意一點，過點P分別作直線y=x和y軸的垂線，垂足分別為M、N.
（1）求證：
是定值；
（2）判斷并說明
有最大值還是最小值，并求出此最大值或最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數
（
）.
（1）證明：當
時，
在
上是減函數，在
上是增函數，并寫出當
時的單調區間；
（2）已知函數
，函數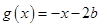
，若對任意
，總存在
，使得
成立，求實數
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
定義在
上的函數
，如果滿足：對任意
，存在常數
，都有
成立，則稱是上的有界函數，其中
稱為函數的一個上界.
已知函數
，
.
（1）若函數
為奇函數，求實數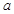
的值；
（2）在（1）的條件下，求函數在區間
上的所有上界構成的集合；
（3）若函數在
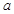上是以3為上界的有界函數，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
設定義域為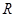
的函數
（Ⅰ）在平面直角坐標系內作出函數
的圖象，并指出的單調區間（不需證明）；
（Ⅱ）若方程
有兩個解，求出
的取值范圍（只需簡單說明，不需嚴格證明）.
（Ⅲ）設定義為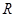的函數
為奇函數，且當
時，
求的解析式.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
上海某化學試劑廠以x千克/小時的速度生產某種產品（生產條件要求
），為了保證產品的質量，需要一邊生產一邊運輸，這樣按照目前的市場價格，每小時可獲得利潤是
元.
(1)要使生產運輸該產品2小時獲得的利潤不低于3000元，求x的取值范圍；
(2)要使生產運輸900千克該產品獲得的利潤最大，問：該工廠應該選取何種生產速度？并求最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
