Question

用秦九韶算法求多項式f（x）=8x⁷+5x⁶+3x⁴+2x+1，當x=2時的值．

Answer 1

【答案】分析：利用秦九韶算法一步一步地代入運算，注意本題中有幾項不存在，此時在計算時，我們應該將這些項加上，比如含有x³這一項可看作0•x³．
解答：解：根據秦九韶算法，把多項式改寫成如下形式
f（x）=8x⁷+5x⁶+0•x⁵+3•x⁴+0•x³+0•x²+2x+1
=（（（（（（8x+5）x+0）x+3）x+0）x+0）x+2）x+1
v=8，v₁=8×2+5=21
v₂=21×2+0=42，v₃=42×2+3=87
v₄=87×2+0=174，v₅=174×2+0=348
v₆=348×2+2=698，v₇=698×2+1=1397．
∴當x=2時，多項式的值為1397．
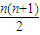
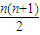點評：一般地，一元n次多項式的求值需要經過次乘法和n次加法，而秦九韶算法只需要n次乘法和n次加法．