
【題目】已知![]() 的內角
的內角![]() ,
,![]() ,
,![]() 的對邊分別為
的對邊分別為![]() ,
,![]() ,
,![]() ,且滿足
,且滿足![]() .
.
(Ⅰ)求角![]() ;
;
(Ⅱ)向量![]() ,
,![]() ,若函數
,若函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,求角
對稱,求角![]() 、
、![]() .
.
科目:高中數學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝![]() 臺發電機的水電站,過去
臺發電機的水電站,過去![]() 年的水文資料顯示,水庫年入流量
年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和.單位:億立方米)都在40以上,不足
(年入流量:一年內上游來水與庫區降水之和.單位:億立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超過
且不超過![]() 的年份有
的年份有![]() 年,超過
年,超過![]() 的年份有
的年份有![]() 年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來![]() 年中,設
年中,設![]() 表示流量超過
表示流量超過![]() 的年數,求
的年數,求![]() 的分布列及期望;
的分布列及期望;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系:
限制,并有如下關系:
年入流量 |
|
|
|
發電機最多可運行臺數 |
|
|
|
若某臺發電機運行,則該臺年利潤為![]() 萬元,若某臺發電機未運行,則該臺年虧損
萬元,若某臺發電機未運行,則該臺年虧損![]() 萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地政府鑒于某種日常食品價格增長過快,欲將這種食品價格控制在適當范圍內,決定對這種食品生產廠家提供政府補貼,設這種食品的市場價格為x元/千克,政府補貼為t元/千克,根據市場調查,當16≤x≤24時,這種食品市場日供應量p萬千克與市場日需求量q萬千克近似地滿足關系:p=2(x+4t-14)(x≥16,t≥0),q=24+8ln ![]() (16≤x≤24).當p=q時的市場價格稱為市場平衡價格.
(16≤x≤24).當p=q時的市場價格稱為市場平衡價格.
(1)將政府補貼表示為市場平衡價格的函數,并求出函數的值域.
(2)為使市場平衡價格不高于每千克20元,政府補貼至少為每千克多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線y=Asin(ωx+φ)(A>0,ω>0)上的一個最高點的坐標為(![]() ,
,![]() ),由此點到相鄰最低點間的曲線與x軸交于點(
),由此點到相鄰最低點間的曲線與x軸交于點(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求這條曲線的函數解析式;
(2)寫出函數的單調區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了監控某種零件的一條生產線的生產過程,檢驗員每天從該生產線上隨機抽取16個零件,并測量其尺寸(單位:cm).根據長期生產經驗,可以認為這條生產線正常狀態下生產的零件的尺寸服從正態分布![]() .
.
(1)假設生產狀態正常,記X表示一天內抽取的16個零件中其尺寸在![]()
之外的零件數,求![]() ;
;
(2)一天內抽檢零件中,如果出現了尺寸在![]() 之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
之外的零件,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對當天的生產過程進行檢查.
下面是檢驗員在一天內抽取的16個零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
經計算得![]() ,
, 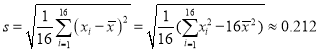 ,其中
,其中![]() 為抽取的第
為抽取的第![]() 個零件的尺寸,
個零件的尺寸, ![]() .
.
用樣本平均數![]() 作為
作為![]() 的估計值
的估計值![]() ,用樣本標準差
,用樣本標準差![]() 作為
作為![]() 的估計值
的估計值![]() ,利用估計值判斷是否需對當天的生產過程進行檢查?剔除
,利用估計值判斷是否需對當天的生產過程進行檢查?剔除![]() 之外的數據,用剩下的數據估計
之外的數據,用剩下的數據估計![]() 和
和![]() (精確到0.01).
(精確到0.01).
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】產品的廣告費支出x與銷售額y(單位:百萬元)之間有如下對應數據:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)畫出散點圖.
(2)求回歸方程.
(3)試預測廣告費支出為10百萬元時,銷售額多大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的離心率為
)的離心率為![]() ,直線
,直線![]() :
: ![]() 與以原點為圓心、橢圓
與以原點為圓心、橢圓![]() 的短半軸長為半徑的圓
的短半軸長為半徑的圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的左頂點
的左頂點![]() 作直線
作直線![]() ,與圓
,與圓![]() 相交于兩點
相交于兩點![]() ,
, ![]() ,若
,若![]() 是鈍角三角形,求直線
是鈍角三角形,求直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com