
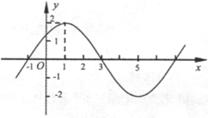
已知函數(shù)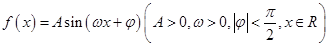 的圖象的一部分如圖所示.
的圖象的一部分如圖所示.
(1)求函數(shù)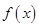 的解析式;
的解析式;
(2)當(dāng)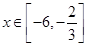 時(shí),求函數(shù)
時(shí),求函數(shù)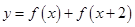 的最大值與最小值及相應(yīng)的
的最大值與最小值及相應(yīng)的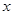 的值.
的值.
(1)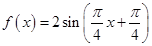 ;
;
(2)當(dāng)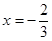 時(shí),
時(shí),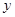 的最大值為
的最大值為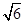 ;當(dāng)
;當(dāng)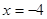 時(shí),
時(shí),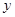 的最小值
的最小值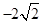 .
.
【解析】
試題分析:(1)先根據(jù)圖象得出最大值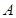 ,以及周期,從而求出
,以及周期,從而求出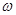 的值,最后將最高點(diǎn)
的值,最后將最高點(diǎn)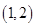 代入函數(shù)解析式并結(jié)合
代入函數(shù)解析式并結(jié)合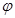 的取值范圍得出
的取值范圍得出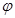 的值,從而確定函數(shù)
的值,從而確定函數(shù)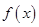 的解析式;(2)求出函數(shù)
的解析式;(2)求出函數(shù)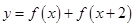 結(jié)合誘導(dǎo)公式以及輔助角公式將函數(shù)
結(jié)合誘導(dǎo)公式以及輔助角公式將函數(shù)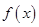 的解析式化簡為
的解析式化簡為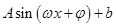 的形式,并計(jì)算出
的形式,并計(jì)算出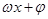 的取值范圍,然后結(jié)合正弦曲線得到函數(shù)的最值,并找出相應(yīng)的最值時(shí),
的取值范圍,然后結(jié)合正弦曲線得到函數(shù)的最值,并找出相應(yīng)的最值時(shí),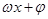 的值,從而求解出函數(shù)取最值時(shí)的
的值,從而求解出函數(shù)取最值時(shí)的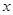 值.
值.
試題解析:(1)由圖像知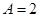 ,
,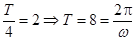 ,∴
,∴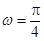 ,得
,得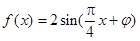 .
.
將最高點(diǎn)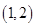 代入,得
代入,得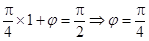 ,
,
∴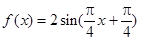 ;
;
(2)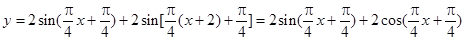
=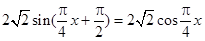 ,
,
∵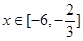 ,∴
,∴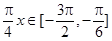 ,
,
∴當(dāng)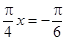 ,即
,即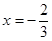 時(shí),
時(shí),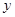 的最大值為
的最大值為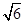 ;當(dāng)
;當(dāng)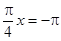 ,即
,即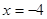 時(shí),
時(shí),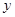 的最小值
的最小值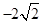 .
.
考點(diǎn):1.三角函數(shù)圖象與三角函數(shù)解析式;2.三角函數(shù)的最值


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:廣西桂林中學(xué)09-10學(xué)年第二學(xué)期高一期中考試 題型:解答題
.
如圖,某市擬在長為8km的道路OP的一側(cè)修建一條運(yùn)動(dòng)賽道,賽道的前一部分為曲線段OSM,該曲線段為函數(shù)y=Asin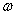 x(A>0,
x(A>0,
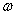 >0) x
>0) x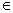 [0,4]的圖象,且圖象的最高點(diǎn)為S(3,2
[0,4]的圖象,且圖象的最高點(diǎn)為S(3,2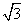 );賽道的后一部分為折線段MNP,為保證參賽運(yùn)動(dòng)員的安全,限定
);賽道的后一部分為折線段MNP,為保證參賽運(yùn)動(dòng)員的安全,限定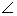 MNP=120
MNP=120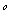
(I)求A , 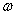 的值和M,P兩點(diǎn)間的距離;
的值和M,P兩點(diǎn)間的距離;
(II)應(yīng)如何設(shè)計(jì),才能使折線段賽道MNP最長?(已知在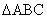 中
中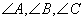 所對(duì)的邊分別為
所對(duì)的邊分別為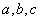 ;滿足:
;滿足: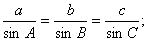
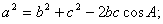
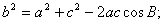
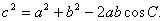 )
)

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com