已知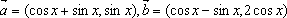
，設
．
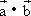(1)求函數
f(x)的單調增區間；(2)三角形
ABC的三個角A，B，C所對邊分別是a，b，c，且滿足A＝
，f(B)＝1，
a＋
b＝10，求邊c．
第三學期贏在暑假系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目：高中數學 來源：江西省南昌市2011屆高三第二次模擬考試數學理科試題 題型：044
已知
，設f(x)＝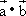
．
(1)求函數f(x)的單調增區間；(2)三角形ABC的三個角A，B，C所對邊分別是a，b，c，且滿足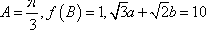
，求邊c．
查看答案和解析>>
科目：高中數學 來源： 題型：
已知冪函數f(x)＝x－m2＋2m＋3(m∈Z)為偶函數，且在區間(0，＋∞)上是單調增函數．
(1)求函數f(x)的解析式；
(2)設函數g(x)＝
＋2x＋c，若g(x)>2對任意的x∈R恒成立，求實數c的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
設α∈{－2，－1，－，，1,2,3}，已知冪函數f(x)＝xα是偶函數，且在區間(0，＋∞)上是減函數，則滿足條件的α值的個數是( )
A．1 B．2 C．3 D．4
查看答案和解析>>
科目：高中數學 來源：2011-2012學年河北省高三8月月考理科數學試卷（解析版） 題型：解答題
已知函數 f(x)＝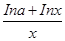
在[1，＋∞)上為減函數，求實數a的取值范圍.
【解析】本試題考查了導數在研究函數中的運用。根據函數f(x)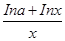＝在[1，＋∞)上為減函數，可知導函數在給定區間恒小于等于零，f ′(x)≤0在[1，＋∞)上恒成立，lna≥1－lnx在[1，＋∞)上恒成立．然后利用φ(x)＝1－lnx，φ(x)max＝1，從而得到a≥e
f ′(x)＝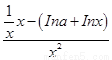
＝
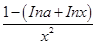，因為 f(x)在[1，＋∞)上為減函數，故 f ′(x)≤0在[1，＋∞)上恒成立，即lna≥1－lnx在[1，＋∞)上恒成立．設φ(x)＝1－lnx，φ(x)max＝1，故lna≥1，a≥e，
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
