
【題目】在直角坐標系xOy中,曲線C1的參數方程為 ![]() (t為參數),以原點O為極點,以x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=﹣
(t為參數),以原點O為極點,以x軸正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=﹣ ![]() .
.
(1)求曲線C1的普通方程與曲線C2的直角坐標方程;
(2)若C1上的點P對應的參數為t= ![]() ,Q為C2上的動點,求PQ中點M到直線C3:
,Q為C2上的動點,求PQ中點M到直線C3: ![]() (α為參數)距離的最小值.
(α為參數)距離的最小值.
【答案】
(1)解:∵曲線C1的參數方程為 ![]() (t為參數),
(t為參數),
∴ ![]() ,
,
∴曲線C1的普通方程為(x+4)2+(y﹣3)2=1.
∵曲線C2的極坐標方程為ρ=﹣ ![]() ,
,
∴ρ2+8ρ2sin2θ=36,∴x2+y2+8y2=36,
∴曲線C2的直角坐標方程為 ![]() =1
=1
(2)解:∵C1上的點P對應的參數為t= ![]() ,∴P(﹣4,4),
,∴P(﹣4,4),
∵Q為C2上的動點,∴Q(6cosθ,2sinθ),
∴PQ中點M(﹣2+3cosθ,2+sinθ),
∵直線C3: ![]() (α為參數),
(α為參數),
∴C3為直線x+ ![]() y+6
y+6 ![]() =0,
=0,
∴點M到C1的距離:
d= ![]() =|4
=|4 ![]() |,
|,
∴當sin( ![]() )=﹣1時,PQ中點M到直線C3:
)=﹣1時,PQ中點M到直線C3: ![]() (α為參數)距離的最小值:
(α為參數)距離的最小值:
dmin=3 ![]() ﹣1
﹣1
【解析】(1)曲線C1的參數方程中利用sin2t+cos2t=1,消去參數t,能求出曲線C1的普通方程;曲線C2的極坐標方程中利用ρ2=x2+y2 , y=ρsinθ,能求出曲線C2的直角坐標方程.(2)先求出P(﹣4,4),Q(6cosθ,2sinθ),從而求出PQ中點M的坐標,再求出直線C3的直角坐標方程,由此利用點到直線的距離公式能求出PQ中點M到直線C3的距離的最小值.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來蓬勃發展的新機遇相關管理部門推出了針對電商的商品和服務的評價體系.現從評價系統中選出![]() 次成功交易,并對其評價進行統計愛,商品和服務評價的
次成功交易,并對其評價進行統計愛,商品和服務評價的![]() 列聯表如下表:
列聯表如下表:
對服務好評 | 對服務不滿意 | 合計 | |
對商品好評 |
|
|
|
對商品不滿意 |
|
|
|
合計 |
|
|
|
(1)是否可以在犯錯誤概率不超過![]() 的前提下,認為商品好評與服務好評有關?
的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的![]() 次購物中,設對商品和服務全好評的次數為隨機變量
次購物中,設對商品和服務全好評的次數為隨機變量![]() ,求
,求![]() 的數學期望.
的數學期望.
參考數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(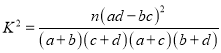 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某批發市場對某種商品的日銷售量(單位:噸)進行統計,最近50天的統計結果如下:

若以上表中頻率作為概率,且每天的銷售量相互獨立.
(1)求5天中該種商品恰好有兩天的日銷售量為1.5噸的概率;
(2)已知每噸該商品的銷售利潤為2千元, ![]() 表示該種商品某兩天銷售利潤的和(單位:千元),求
表示該種商品某兩天銷售利潤的和(單位:千元),求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某天連續有![]() 節課,其中語文、英語、物理、化學、生物
節課,其中語文、英語、物理、化學、生物![]() 科各
科各![]() 節,數學
節,數學![]() 節.在排課時,要求生物課不排第
節.在排課時,要求生物課不排第![]() 節,數學課要相鄰,英語課與數學課不相鄰,則不同排法的種數是( )
節,數學課要相鄰,英語課與數學課不相鄰,則不同排法的種數是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】繼共享單車之后,又一種新型的出行方式------“共享汽車”也開始亮相北上廣深等十余大中城市,一款叫“一度用車”的共享汽車在廣州提供的車型是“奇瑞eQ”,每次租車收費按行駛里程加用車時間,標準是“1元/公里+0.1元/分鐘”,李先生家離上班地點10公里,每天租用共享汽車上下班,由于堵車因素,每次路上開車花費的時間是一個隨機變量,根據一段時間統計40次路上開車花費時間在各時間段內的情況如下:
時間(分鐘) |
|
|
|
|
|
次數 | 8 | 14 | 8 | 8 | 2 |
以各時間段發生的頻率視為概率,假設每次路上開車花費的時間視為用車時間,范圍為![]() 分鐘.
分鐘.
(Ⅰ)若李先生上.下班時租用一次共享汽車路上開車不超過45分鐘,便是所有可選擇的交通工具中的一次最優選擇,設![]() 是4次使用共享汽車中最優選擇的次數,求
是4次使用共享汽車中最優選擇的次數,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽車2次,一個月(以20天計算)平均用車費用大約是多少(同一時段,用該區間的中點值作代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() (a>b>0)的左、右焦點分別為F1,F2,點M(0,2)是橢圓的一個頂點,△F1MF2是等腰直角三角形.
(a>b>0)的左、右焦點分別為F1,F2,點M(0,2)是橢圓的一個頂點,△F1MF2是等腰直角三角形.
(1)求橢圓的方程;
(2)過點M分別作直線MA,MB交橢圓于A,B兩點,設兩直線的斜率分別為k1,k2,且k1+k2=8,證明:直線AB過定點![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)滿足f(x)=f′(1)ex﹣1﹣f(0)x+ ![]() x2;
x2;
(1)求f(x)的解析式及單調區間;
(2)若 ![]() ,求(a+1)b的最大值.
,求(a+1)b的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com