
已知函數![]() .
.
(1)求f(![]() )+f(-
)+f(-![]() )的值;
)的值;
(2)當x∈![]() (其中a∈(0, 1), 且a為常數)時,
(其中a∈(0, 1), 且a為常數)時,
f(x)是否存在最小值, 若存在, 求出最小值; 若不存在, 請說明理由.
(1)0,(2)當x∈![]() (其中a∈(0, 1), 且a為常數)時,
(其中a∈(0, 1), 且a為常數)時,
f(x)存在最小值,,且最小值為f(a)= -a+log2![]()
(1)f(x)的定義域是(-1, 1),
∵f(-x)=-(-x) +log2![]() =-(-x+log2
=-(-x+log2![]() )=- f(x)
)=- f(x)
∴f(x)為奇函數. ∴f(![]() )+f(-
)+f(-![]() )=0. ……5分
)=0. ……5分
(直接運算也可以)
(2)設-1< x1< x2 <1,
∵f(x2)-f(x1)= - x2+ log2![]() -[- x1+ log2
-[- x1+ log2![]() ] ……7分
] ……7分
=( x1- x2)+ log2![]() ,
,
∵x1- x2< 0, 1+x1-x2- x1x2-(1+x2-x1- x1x2)=2(x1- x2)<0,
∴1+x1-x2- x1x2< 1+x2-x1- x1x2.
∴0<![]() <1.
<1.
∴log2![]() < 0.
< 0.
∴f(x2)-f(x1) < 0. ∴f(x)在(-1, 1)上單調遞減. ……10分
∴當x∈![]() (其中a∈(0, 1), 且a為常數)時,
(其中a∈(0, 1), 且a為常數)時,
f(x)存在最小值,,且最小值為f(a)= -a+log2![]() ……12分
……12分


 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源:2013-2014學年山東省濟南市高三上學期期末考試理科數學試卷(解析版) 題型:解答題
已知函數 .
.
(1)求 的單調區間;
的單調區間;
(2)若 ,
, 在區間
在區間 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆山東省濟寧市高二5月質量檢測理科數學試卷(解析版) 題型:解答題
已知函數 .
.
(1)求 的單調區間;
的單調區間;
(2)當 時,判斷
時,判斷 和
和 的大小,并說明理由;
的大小,并說明理由;
(3)求證:當 時,關于
時,關于 的方程:
的方程: 在區間
在區間 上總有兩個不同的解.
上總有兩個不同的解.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省汕頭市高三畢業班教學質量檢測文科數學(含解析) 題型:解答題
(本題滿分14分)
已知函數 ,
,
(1)求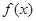 的最小值;
的最小值;
(2)若對所有 都有
都有 ,求實數
,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com