
如圖,點
A在銳二面角α-MN-β的棱MN上,在面α內引射線AP,使AP與MN所成的角∠PAM為45°,與面β所成的二面角大小為30°,求二面角α-MN-β的大小.
|
解:在射線 AP上取一點B,作BH⊥β于H,連結AH,則∠BAH為射線AP與平面β所成的角,∴∠BAH=30°再作BQ⊥AM,交MN于Q,連結HQ,則HQ為BQ在平面β內的射影.由三垂線定理的逆定理,知HQ⊥MN,∴∠ BQH為二面角α-NM-β的平面角.設 BQ=a,在Rt△BAQ中,∠BAQ=90°,∠BAM=45°, , ,
∴在 Rt△ABH中,∠BAH=30°,∴  . .
∴在 Rt△BHQ中,∠BHQ=90°,BQ=a , , ,
∵∠BQH是銳角,∴∠BQH=45°,即二面角α-NM-β等于45° |
|
首先根據條件作出二面角的平面角,然后將平面角放入一個可解的三角形中 (最好是直角三角形),通過解三角形使問題得到解決.本題綜合性較強,在一個圖形中出現了兩條直線所成的角,斜線與平面所成的角,二面角等空間角,這些空間角都要轉化為平面角,而且還要彼此聯系相互依存,要根據各自的定義添加適當的輔助線. |


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數學 來源: 題型:
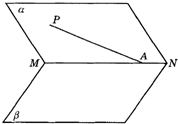 如圖,點A在銳二面角α-MN-β的棱MN上,在面α內引射線AP,使AP與MN所成的∠PAM為45°,與面β所成的角為30°,求二面角α-MN-β的大小
如圖,點A在銳二面角α-MN-β的棱MN上,在面α內引射線AP,使AP與MN所成的∠PAM為45°,與面β所成的角為30°,求二面角α-MN-β的大小查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044
如圖,點A在銳二面角α-MN-β的棱MN上,在面α內引射線AP,使AP與MN所成的角∠PAM為45°,與面β所成的二面角大小為30°,求二面角α-MN-β的大小.

查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省撫州市廣昌一中、崇仁一中高二(上)期中數學試卷(理科)(解析版) 題型:填空題

查看答案和解析>>
科目:高中數學 來源:2010-2011學年吉林省長春市十一中高一(下)期末數學試卷(文科)(解析版) 題型:填空題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com