
已知函數(shù)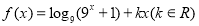 是偶函數(shù)
是偶函數(shù)
(1)求k的值;
(2)若函數(shù) 的圖象與直線
的圖象與直線 沒有交點,求b的取值范圍;
沒有交點,求b的取值范圍;
(3)設(shè) ,若函數(shù)
,若函數(shù) 與
與 的圖象有且只有一個公共點,求實數(shù)
的圖象有且只有一個公共點,求實數(shù) 的取值范圍
的取值范圍
(1)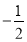 ;(2)
;(2)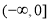 ;(3)
;(3) 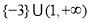
【解析】
試題分析:(1)因為函數(shù)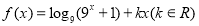 是偶函數(shù),所以根據(jù)偶函數(shù)的定義,得到一個關(guān)于x,k的等式.由于對于任意的x都成立,相當(dāng)于恒過定點的問題,所以求得k的值.
是偶函數(shù),所以根據(jù)偶函數(shù)的定義,得到一個關(guān)于x,k的等式.由于對于任意的x都成立,相當(dāng)于恒過定點的問題,所以求得k的值.
(2)因為函數(shù)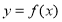 的圖象與直線
的圖象與直線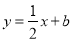 沒有交點,所以對應(yīng)的方程沒有解,利用分離變量的思維可得到一個等式
沒有交點,所以對應(yīng)的方程沒有解,利用分離變量的思維可得到一個等式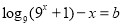 ,該方程無解.所以等價兩個函數(shù)
,該方程無解.所以等價兩個函數(shù)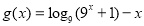 與
與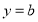 沒有交點,所以求出函數(shù)
沒有交點,所以求出函數(shù)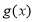 的最值.即可得到b的取值范圍.
的最值.即可得到b的取值范圍.
(3)因為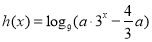 ,若函數(shù)
,若函數(shù)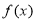 與
與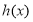 的圖象有且只有一個公共點,所以等價于方程
的圖象有且只有一個公共點,所以等價于方程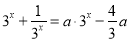 有且只有一個實數(shù)根.通過換元
有且只有一個實數(shù)根.通過換元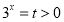 將原方程化為含參的二次方程的形式,即等價于該二次方程僅有一個大于零的實根,通過討論即可得到結(jié)論.
將原方程化為含參的二次方程的形式,即等價于該二次方程僅有一個大于零的實根,通過討論即可得到結(jié)論.
試題解析:(1)因為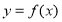 為偶函數(shù),所以
為偶函數(shù),所以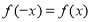 ,
,
即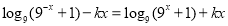 對于任意
對于任意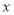 恒成立.
恒成立.
于是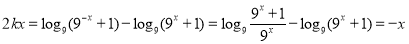 恒成立,
恒成立,
而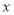 不恒為零,所以
不恒為零,所以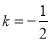 . 4分
. 4分
(2)由題意知方程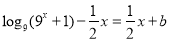 即方程
即方程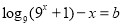 無解.
無解.
令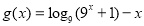 ,則函數(shù)
,則函數(shù)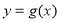 的圖象與直線
的圖象與直線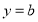 無交點.
無交點.
因為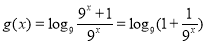 ,由
,由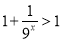 ,則
,則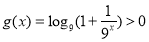 ,
,
所以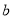 的取值范圍是
的取值范圍是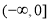 . 8分
. 8分
(3)由題意知方程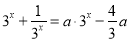 有且只有一個實數(shù)根.
有且只有一個實數(shù)根.
令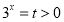 ,則關(guān)于
,則關(guān)于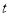 的方程
的方程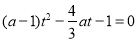 (記為(*))有且只有一個正根.
(記為(*))有且只有一個正根.
若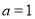 ,則
,則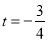 ,不合題意, 舍去;
,不合題意, 舍去;
若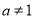 ,則方程(*)的兩根異號或有兩相等正根.
,則方程(*)的兩根異號或有兩相等正根.
由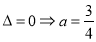 或
或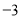 ;但
;但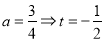 ,不合題意,舍去;而
,不合題意,舍去;而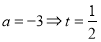 ;
;
若方程(*)的兩根異號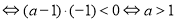
綜上所述,實數(shù) 的取值范圍是
的取值范圍是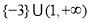 . 12分
. 12分
考點:1.函數(shù)的奇偶性.2.函數(shù)的與方程的思想的轉(zhuǎn)化.3.換元法的應(yīng)用.4.含參數(shù)的方程的根的討論.


科目:高中數(shù)學(xué) 來源:2016屆黑龍江省高一上學(xué)期期末數(shù)學(xué)試卷(解析版) 題型:選擇題
在平行四邊形 中,
中,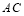 與
與 交于點
交于點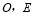 是線段
是線段 的中點,
的中點,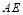 的延長線與
的延長線與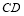 交于點
交于點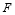 ,若
,若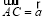 ,
, ,則
,則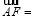 ( )
( )
A.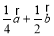 B.
B.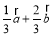 C.
C.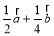 D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆陜西寶雞金臺區(qū)高一上學(xué)期期末檢測數(shù)學(xué)試卷(解析版) 題型:選擇題
長方體的一個頂點上三條棱長分別是3、4、5,且它的八個頂點都在同一球面上,這個球的表面積是( )
A.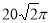 B.
B.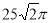
C.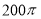 D.
D.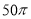
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆遼寧省高一下學(xué)期期初入學(xué)考試數(shù)學(xué)試卷(解析版) 題型:選擇題
設(shè)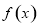 是
是 上的奇函數(shù),且
上的奇函數(shù),且 時,
時, ,對任意
,對任意 ,不等式
,不等式 恒成立,則
恒成立,則 的取值范圍( )
的取值范圍( )
A. B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆遼寧省高一下學(xué)期期初入學(xué)考試數(shù)學(xué)試卷(解析版) 題型:選擇題
直三棱柱各側(cè)棱和底面邊長均為 ,點
,點 是
是 上任意一點,連接
上任意一點,連接 ,
,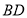 ,
, ,
, ,則三棱錐
,則三棱錐 的體積為( )
的體積為( )
A. B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆遼寧省五校高一上學(xué)期期末聯(lián)考數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù)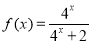
(1)若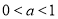 ,求
,求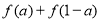 的值;
的值;
(2)求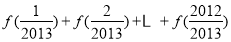 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆遼寧省五校高一上學(xué)期期末聯(lián)考數(shù)學(xué)試卷(解析版) 題型:選擇題
已知 為偶函數(shù),當(dāng)
為偶函數(shù),當(dāng) 時,
時, ,滿足
,滿足 的實數(shù)
的實數(shù) 的個數(shù)為( )
的個數(shù)為( )

(A)2 (B) 4 (C) 6 (D) 8
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆遼寧大連教育學(xué)院高一第一學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:填空題
如圖所示,三棱柱 ,則
,則 .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2016屆貴州省黔東南州高一上學(xué)期期末考試數(shù)學(xué)試卷(解析版) 題型:解答題
本小題滿分10分)已知集合 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,且
,且 ,求實數(shù)
,求實數(shù) 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com