
【題目】已知拋物線![]() 的焦點
的焦點![]() 也是橢圓
也是橢圓![]() 的一個焦點,
的一個焦點,![]() 與
與![]() 的公共弦的長為
的公共弦的長為![]() .
.
(1)求![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,與
兩點,與![]() 相交于
相交于![]() ,
,![]() 兩點,且
兩點,且![]() 與
與![]() 同向
同向
(ⅰ)若![]() ,求直線
,求直線![]() 的斜率
的斜率
(ⅱ)設![]() 在點
在點![]() 處的切線與
處的切線與![]() 軸的交點為
軸的交點為![]() ,證明:直線
,證明:直線![]() 繞點
繞點![]() 旋轉時,
旋轉時,![]() 總是鈍角三角形
總是鈍角三角形
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() ,(ii)詳見解析.
,(ii)詳見解析.
【解析】
試題分析:(1)根據已知條件可求得![]() 的焦點坐標為
的焦點坐標為![]() ,再利用公共弦長為
,再利用公共弦長為![]() 即可求解;(2)(i)設直線
即可求解;(2)(i)設直線![]() 的斜率為
的斜率為![]() ,則
,則![]() 的方程為
的方程為![]() ,由
,由![]() 得
得![]() ,根據條件可知
,根據條件可知![]()
![]() ,從而可以建立關于
,從而可以建立關于![]() 的方程,即可求解;(ii)根據條件可說明
的方程,即可求解;(ii)根據條件可說明![]()
![]()
![]() ,因此
,因此![]() 是銳角,從而
是銳角,從而![]() 是鈍角,即可得證
是鈍角,即可得證
試題解析:(1)由![]() :
:![]() 知其焦點
知其焦點![]() 的坐標為
的坐標為![]() ,∵
,∵![]() 也是橢圓
也是橢圓![]() 的一焦點,
的一焦點,
∴ ![]() ①,又
①,又![]() 與
與![]() 的公共弦的長為
的公共弦的長為![]() ,
,![]() 與
與![]() 都關于
都關于![]() 軸對稱,且
軸對稱,且![]() 的方程為
的方程為![]() ,由此易知
,由此易知![]() 與
與![]() 的公共點的坐標為
的公共點的坐標為![]() ,∴
,∴![]() ②,聯立①,②,得
②,聯立①,②,得![]() ,
,![]() ,故
,故![]() 的方程為
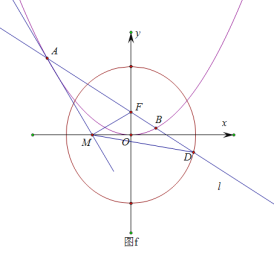
的方程為![]() ;(2)如圖
;(2)如圖![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(i)∵![]() 與
與![]() 同向,且
同向,且![]() ,∴
,∴![]()
![]() ,從而
,從而![]()
![]() ,即
,即![]()
![]() ,于是
,于是![]()
![]()
![]()
![]() ③,設直線
③,設直線![]() 的斜率為
的斜率為![]() ,則
,則![]() 的方程為
的方程為![]() ,由
,由![]() 得
得![]() ,而
,而![]() ,
,![]() 是這個方程的兩根,∴
是這個方程的兩根,∴![]() ,
,![]() ④,由
④,由 得
得![]() ,而
,而![]() ,
,![]() 是這個方程的兩根,∴
是這個方程的兩根,∴![]()
![]() ,
,![]()
![]() ⑤,將④⑤帶入③,得
⑤,將④⑤帶入③,得![]() ,即
,即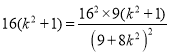 ,
,
∴![]()
![]() ,解得
,解得![]() ,即直線
,即直線![]() 的斜率為
的斜率為![]() .
.
(ii)由![]() 得
得![]()
![]() ,∴
,∴![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,即
,即
![]() ,令
,令![]() ,得
,得![]() ,即
,即![]() ,∴
,∴![]() ,而
,而![]() ,于是
,于是
![]()
![]()
![]() ,因此
,因此![]() 是銳角,從而
是銳角,從而![]() 是鈍角.,故直線
是鈍角.,故直線![]() 繞點
繞點![]() 旋轉時,
旋轉時,![]() 總是鈍角三角形.
總是鈍角三角形.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:
【題目】已知頂點在原點,焦點在x軸上的拋物線被直線y=2x+1截得的弦長為 ![]() .
.
(1)求拋物線的方程;
(2)若拋物線與直線y=2x﹣5無公共點,試在拋物線上求一點,使這點到直線y=2x﹣5的距離最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正三棱柱ABC﹣A1B1C1的棱長都為2,E,F,G為 AB,AA1 , A1C1的中點,則B1F 與面GEF成角的正弦值( )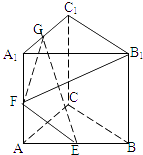
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ).
).
(Ⅰ)若 ![]()
![]() =1,求cos(
=1,求cos( ![]() ﹣x)的值;
﹣x)的值;
(Ⅱ)記f(x)= ![]()
![]() ,在△ABC中,A、B、C的對邊分別為a、b、c,且滿足(2a﹣c)cosB=bcosC,求函數f(A)的取值范圍.
,在△ABC中,A、B、C的對邊分別為a、b、c,且滿足(2a﹣c)cosB=bcosC,求函數f(A)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=log2(1+x)﹣log2(1﹣x),g(x)=log2(1+x)+log2(1﹣x).
(1)判斷函數f(x)奇偶性并證明;
(2)判斷函數f(x)單調性并用單調性定義證明;
(3)求函數g(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
設函數f(x)=alnx﹣bx2(x>0).
(1)若函數f(x)在x=1處于直線![]() 相切,求函數f(x)在
相切,求函數f(x)在![]() 上的最大值;
上的最大值;
(2)當b=0時,若不等式f(x)≥m+x對所有的a∈[1,![]() ],x∈[1,e2]都成立,求實數m的取值范圍.
],x∈[1,e2]都成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com