
如果數(shù)列 滿足:
滿足: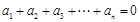 且
且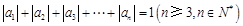 ,則稱數(shù)列
,則稱數(shù)列 為
為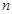 階“歸化數(shù)列”.
階“歸化數(shù)列”.
(1)若某4階“歸化數(shù)列” 是等比數(shù)列,寫出該數(shù)列的各項;
是等比數(shù)列,寫出該數(shù)列的各項;
(2)若某11階“歸化數(shù)列” 是等差數(shù)列,求該數(shù)列的通項公式;
是等差數(shù)列,求該數(shù)列的通項公式;
(3)若 為n階“歸化數(shù)列”,求證:
為n階“歸化數(shù)列”,求證: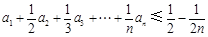 .
.
(1)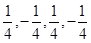 或
或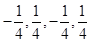 ;(2)
;(2)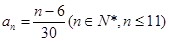 或
或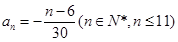 ;(3)證明見解析.
;(3)證明見解析.
解析試題分析:(1)等比數(shù)列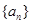 是4階“歸化數(shù)列”,則有
是4階“歸化數(shù)列”,則有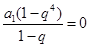 ,這樣
,這樣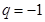 ,于是
,于是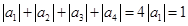 ,從而
,從而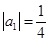 ,
,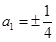 ,以后各項依次可寫出;(2)等差數(shù)列
,以后各項依次可寫出;(2)等差數(shù)列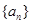 是11階“歸化數(shù)列”,則
是11階“歸化數(shù)列”,則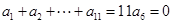 ,
,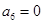 ,這樣有
,這樣有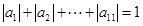 ,知當(dāng)
,知當(dāng)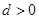 時,
時,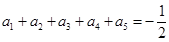 ,當(dāng)
,當(dāng)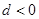 時,
時,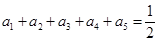 ,由此可得
,由此可得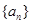 的通項公式分別為
的通項公式分別為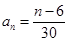 或
或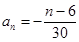 ;(3)對
;(3)對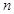 階“歸化數(shù)列”,從已知上我們只能知道在
階“歸化數(shù)列”,從已知上我們只能知道在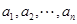 中有正有負,因此為了求
中有正有負,因此為了求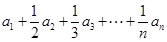 ,我們可以設(shè)
,我們可以設(shè)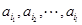 是正的,
是正的,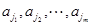 是負的,這樣
是負的,這樣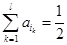 ,
,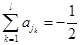 ,
,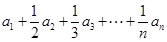
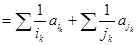
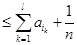
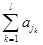
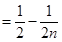
證畢.
(1)設(shè)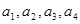 成公比為
成公比為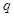 的等比數(shù)列,顯然
的等比數(shù)列,顯然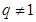 ,則由
,則由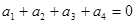 ,
,
得 ,解得
,解得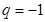 ,由
,由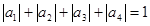 得
得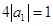 ,解得
,解得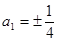 ,
,
所以數(shù)列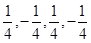 或
或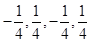 為所求四階“歸化數(shù)列”; 4分
為所求四階“歸化數(shù)列”; 4分
(2)設(shè)等差數(shù)列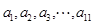 的公差為
的公差為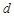 ,由
,由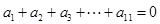 ,
,
所以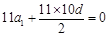 ,所以
,所以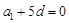 ,即
,即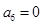 , 6分
, 6分
當(dāng)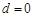 時,與歸化數(shù)列的條件相矛盾,
時,與歸化數(shù)列的條件相矛盾,
當(dāng)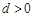 時,由
時,由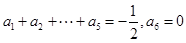 ,所以
,所以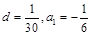 ,
,
所以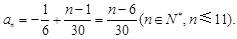 8分
8分
當(dāng)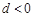 時,由
時,由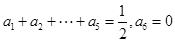 ,所以
,所以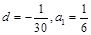 ,
,
所以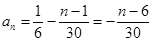 (n∈N*,n≤11),
(n∈N*,n≤11),
所以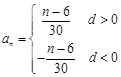 (n∈N*,n≤11), 10分
(n∈N*,n≤11), 10分
(3)由已知可知,必有ai>0,也必有aj<0(i,j∈{1,2, ,n,且i≠j).
設(shè)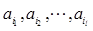 為諸ai中所有大于0的數(shù),
為諸ai中所有大于0的數(shù),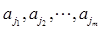 為諸ai中所有小于0的數(shù).
為諸ai中所有小于0的數(shù).
由已知得X=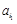 +
+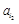 +…+
+…+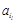 =
=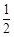 ,Y=
,Y=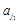 +
+


科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)數(shù)列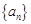 的前
的前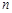 項和為
項和為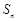 ,且滿足
,且滿足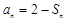
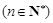 .
.
(1)求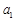 ,
, ,
,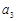 ,
,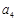 的值并寫出其通項公式;(2)證明數(shù)列
的值并寫出其通項公式;(2)證明數(shù)列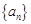 是等比數(shù)列.
是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示的兩個同心圓盤均被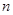 等分(
等分(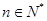 且
且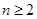 ),在相重疊的扇形格中依次同時填上
),在相重疊的扇形格中依次同時填上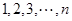 ,內(nèi)圓盤可繞圓心旋轉(zhuǎn),每次可旋轉(zhuǎn)一個扇形格,當(dāng)內(nèi)圓盤旋轉(zhuǎn)到某一位置時,定義所有重疊扇形格中兩數(shù)之積的和為此位置的“旋轉(zhuǎn)和”.
,內(nèi)圓盤可繞圓心旋轉(zhuǎn),每次可旋轉(zhuǎn)一個扇形格,當(dāng)內(nèi)圓盤旋轉(zhuǎn)到某一位置時,定義所有重疊扇形格中兩數(shù)之積的和為此位置的“旋轉(zhuǎn)和”.
(1)求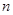 個不同位置的“旋轉(zhuǎn)和”的和;
個不同位置的“旋轉(zhuǎn)和”的和;
(2)當(dāng)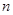 為偶數(shù)時,求
為偶數(shù)時,求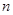 個不同位置的“旋轉(zhuǎn)和”的最小值;
個不同位置的“旋轉(zhuǎn)和”的最小值;
(3)設(shè)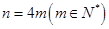 ,在如圖所示的初始位置將任意
,在如圖所示的初始位置將任意 對重疊的扇形格中的兩數(shù)均改寫為0,證明:當(dāng)
對重疊的扇形格中的兩數(shù)均改寫為0,證明:當(dāng)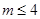 時,通過旋轉(zhuǎn),總存在一個位置,任意重疊的扇形格中兩數(shù)不同時為0.
時,通過旋轉(zhuǎn),總存在一個位置,任意重疊的扇形格中兩數(shù)不同時為0.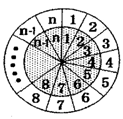
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com