【題目】已知
，將函數
圖象向下平移
個單位得到
的圖象，則
（Ⅰ）求函數
的最小正周期和單調遞增區間；
（Ⅱ）求
在區間
上的取值范圍．
全優點練單元計劃系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的左焦點為
，設
是橢圓
的兩個短軸端點，
是橢圓
的長軸左端點．
（Ⅰ）當
時，設點
，直線
交橢圓
于
，且直線
的斜率分別為
，求
的值；
（Ⅱ）當
時，若經過
的直線
與橢圓
交于
兩點，O為坐標原點，求
與
的面積之差的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
， 
）為奇函數，且相鄰兩對稱軸間的距離為
.
（1）當
時，求
的單調遞減區間；
（2）將函數
的圖象沿
軸方向向右平移
個單位長度，再把橫坐標縮短到原來的
（縱坐標不變），得到函數
的圖象.當
時，求函數
的值域.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學為了解2017屆高三學生的性別和喜愛游泳是否有關，對100名高三學生進行了問卷調查，得到如下列聯表：
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人，抽到喜歡游泳的學生的概率為
．
（Ⅰ）請將上述列聯表補充完整；
（Ⅱ）判斷是否有99.9%的把握認為喜歡游泳與性別有關？
附： 
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某家父母記錄了女兒玥玥的年齡（歲）和身高（單位cm）的數據如下：
年齡x | 6 | 7 | 8 | 9 |
身高y | 118 | 126 | 136 | 144 |
（1）試求y關于x的線性回歸方程 
= 
x+ 
（2）試預測玥玥10歲時的身高．（其中， = 
， = 
﹣ 
．
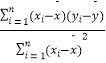查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在棱長為2的正方體
中， 
， 
， 
， 
分別是棱
， 
， 
， 
的中點，點
， 
分別在棱
， 
上移動，且
.
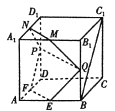
（1）當
時，證明：直線
平面
；
（2）是否存在
，使面
與面
所成的二面角為直二面角？若存在，求出
的值；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為研究男女同學空間想象能力的差異，孫老師從高一年級隨機選取了20名男生、20名女生，進行空間圖形識別測試，得到成績莖葉圖如下，假定成績大于等于80分的同學為“空間想象能力突出”，低于80分的同學為“空間想象能力正常”.
（1）完成下面
列聯表，并判斷是否有
的把握認為“空間想象能力突出”與性別有關；
空間想象能力突出 | 空間想象能力正常 | 合計 | |
男生 | |||
女生 | |||
合計 |
（2）從“空間想象能力突出”的同學中隨機選取男生2名、女生2名，記其中成績超過90分的人數為
，求隨機變量
的分布列和數學期望.
下面公式及臨界值表僅供參考： 
| 0.100 | 0.050 | 0.010 | |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
（
為常數）.
（1）函數
的圖象在點
處的切線與函數
的圖象相切，求實數
的值；
（2）若函數
在定義域上存在單調減區間，求實數
的取值范圍；
（3）若
， 
，且
，都有
成立，求實數
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
