
【題目】已知曲線C的極坐標方程為ρ=6sinθ,以極點O為原點,極軸為x軸的非負半軸建立直角坐標系,直線l的參數方程為 ![]() (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程及直線l的普通方程;
(2)直線l與曲線C交于B,D兩點,當|BD|取到最小值時,求a的值.
【答案】
(1)解:曲線C的極坐標方程為ρ=6sinθ,即ρ2=6ρsinθ,化為直角坐標方程:x2+y2=6y,配方為:x2+(y﹣3)2=9,圓心C(0,3),半徑r=3.
直線l的參數方程為 ![]() (t為參數),消去參數t可得:x﹣ay+a+1=0
(t為參數),消去參數t可得:x﹣ay+a+1=0
(2)解:由直線l經過定點P(﹣1,1),此點在圓的內部,
因此當CP⊥l時,|BD|取到最小值,則kCPkl= ![]() ×kl=﹣1,解得kl=﹣
×kl=﹣1,解得kl=﹣ ![]() .
.
∴ ![]() =﹣
=﹣ ![]() ,解得a=﹣2
,解得a=﹣2
【解析】(1)曲線C的極坐標方程為ρ=6sinθ,即ρ2=6ρsinθ,利用互化公式可得直角坐標方程.直線l的參數方程為 ![]() (t為參數),消去參數t可得普通方程.(2)由直線l經過定點P(﹣1,1),此點在圓的內部,因此當CP⊥l時,|BD|取到最小值,利用kCPkl=﹣1,解得kl , 即可得出.
(t為參數),消去參數t可得普通方程.(2)由直線l經過定點P(﹣1,1),此點在圓的內部,因此當CP⊥l時,|BD|取到最小值,利用kCPkl=﹣1,解得kl , 即可得出.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案科目:高中數學 來源: 題型:
【題目】學校為了對教師教學水平和教師管理水平進行評價,從該校學生中選出300人進行統計.其中對教師教學水平給出好評的學生人數為總數的![]() ,對教師管理水平給出好評的學生人數為總數的
,對教師管理水平給出好評的學生人數為總數的![]() ,其中對教師教學水平和教師管理水平都給出好評的有120人.
,其中對教師教學水平和教師管理水平都給出好評的有120人.
(1)填寫教師教學水平和教師管理水平評價的![]() 列聯表:
列聯表:
對教師管理水平好評 | 對教師管理水平不滿意 | 合計 | |
對教師教學水平好評 | |||
對教師教學水平不滿意 | |||
合計 |
請問是否可以在犯錯誤概率不超過0.001的前提下,認為教師教學水平好評與教師管理水平好評有關?
(2)若將頻率視為概率,有4人參與了此次評價,設對教師教學水平和教師管理水平全好評的人數為隨機變量![]() .
.
①求對教師教學水平和教師管理水平全好評的人數![]() 的分布列(概率用組合數算式表示);
的分布列(概率用組合數算式表示);
②求![]() 的數學期望和方差.
的數學期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在本校任選了一個班級,對全班50名學生進行了作業量的調查,根據調查結果統計后,得到如下的![]() 列聯表,已知在這50人中隨機抽取2人,這2人都“認為作業量大”的概率為
列聯表,已知在這50人中隨機抽取2人,這2人都“認為作業量大”的概率為![]() .
.
| 認為作業量大 | 認為作業量不大 | 合計 |
男生 | 18 | ||
女生 | 17 | ||
合計 | 50 |
(Ⅰ)請完成上面的列聯表;
(Ⅱ)根據列聯表的數據,能否有![]() 的把握認為“認為作業量大”與“性別”有關?
的把握認為“認為作業量大”與“性別”有關?
(Ⅲ)若視頻率為概率,在全校隨機抽取4人,其中“認為作業量大”的人數記為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() ,以原點為極點,
,以原點為極點,![]() 軸正半軸為極軸建立極坐標系,圓
軸正半軸為極軸建立極坐標系,圓![]() 極坐標方程為
極坐標方程為![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求
相切,求![]() 的值;
的值;
(2)已知直線![]() 與圓
與圓![]() 交于
交于![]() ,
,![]() 兩點,記點
兩點,記點![]() 、
、![]() 相應的參數分別為
相應的參數分別為![]() ,
,![]() ,當
,當![]() 時,求
時,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】執行如圖的程序框圖,當n≥2,n∈Z時,fn(x)表示fn﹣1(x)的導函數,若輸入函數f1(x)=sinx﹣cosx,則輸出的函數fn(x)可化為( ) 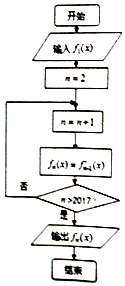
A.![]() sin(x+
sin(x+ ![]() )
)
B.![]() sin(x﹣
sin(x﹣ ![]() )??
)??
C.﹣ ![]() sin(x+
sin(x+ ![]() )
)
D.﹣ ![]() sin(x﹣
sin(x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
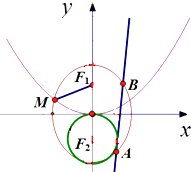
【題目】已知F1 , F2分別為橢圓C1: ![]() (a>b>0)的上下焦點,其F1是拋物線C2:x2=4y的焦點,點M是C1與C2在第二象限的交點,且|MF1|=
(a>b>0)的上下焦點,其F1是拋物線C2:x2=4y的焦點,點M是C1與C2在第二象限的交點,且|MF1|= ![]() .
. 
(1)試求橢圓C1的方程;
(2)與圓x2+(y+1)2=1相切的直線l:y=k(x+t)(t≠0)交橢圓于A,B兩點,若橢圓上一點P滿足 ![]() ,求實數λ的取值范圍.
,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了分析在一次數學競賽中甲、乙兩個班的數學成績,分別從甲、乙兩個班中隨機抽取了10個學生的成績,成績的莖葉圖如下:

(Ⅰ)根據莖葉圖,計算甲班被抽取學生成績的平均值![]() 及方差
及方差![]() ;
;
(Ⅱ)若規定成績不低于90分的等級為優秀,現從甲、乙兩個班級所抽取成績等級為優秀的學生中,隨機抽取2人,求這兩個人恰好都來自甲班的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com