
(1)當cosθ=0時,判斷函數f(x)是否有極值;
(2)要使函數f(x)的極小值大于零,求參數θ的取值范圍;
(3)若對(2)中所求的取值范圍內的任意參數θ,函數f(x)在區間(2a-1,a)內都是增函數,求實數a的取值范圍.
解:(1)當cosθ=0時,f(x)=4x3,則f(x)在(-∞,+∞)內是增函數,故無極值.
(2)f′(x)=12x2-6xcosθ,令f′(x)=0,得x1=0,x2=![]() .
.
由(1),只需分下面兩種情況討論:
①當cosθ>0時,隨x的變化,f′(x)的符號及f(x)的變化情況如下表:
x | (-∞,0) | 0 | (0, |
| ( |
f′(x) | + | 0 | - | 0 | + |
f(x) | ?↗ | 極大值 | ↙? | 極小值 | ↗? |
因此,函數f(x)在x=![]() 處取得極小值f(
處取得極小值f(![]() ),
),
且f(![]() )=-
)=-![]() cos3θ+
cos3θ+![]() cosθ.
cosθ.
要使f(![]() )>0,必有-
)>0,必有-![]() cosθ(cos2θ-
cosθ(cos2θ-![]() )>0,
)>0,
可得0<cosθ<![]() ;
;
由于0≤θ≤2π,故![]() <θ<
<θ<![]() 或
或![]() <θ<
<θ<![]() .
.
②當cosθ<0時,隨x的變化,f′(x)的符號及f(x)的變化情況如下表:
x | (-∞, |
| ( | 0 | (0,+∞) |
f′(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 極大值 | ?↘ | 極小值 | ↗? |
因此函數f(x)在x=0處取得極小值f(0),且f(0)=![]() cosθ.
cosθ.
若f(0)>0,則cosθ>0,矛盾,所以當cosθ<0時,f(x)的極小值不會大于零.
綜上,要使函數f(x)在(-∞,+∞)內的極小值大于零,參數θ的取值范圍為(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() ).
).
(3)由(2)知,函數f(x)在區間(-∞,0)與(![]() ,+∞)內都是增函數,
,+∞)內都是增函數,
由題設,函數f(x)在(2a-1,a)內是增函數,則a需滿足不等式組
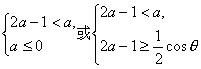
由(2),參數θ∈(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() )時,0<cosθ<
)時,0<cosθ<![]() ,要使不等式2a-1
,要使不等式2a-1![]()
![]() 關于參數θ恒成立,必有2a-1≥
關于參數θ恒成立,必有2a-1≥![]() ,即
,即![]() ≤a.
≤a.
綜上,解得a≤0或![]() ≤a<1,
≤a<1,
所以a的取值范圍是(-∞,0]∪[![]() ,1).
,1).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
|
| 1 |
| 8 |
| f(x1)-f(x2) |
| x1-x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com