
本小題滿分10分)
已知直線l經(jīng)過點(diǎn)P(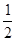 ,1),傾斜角
,1),傾斜角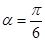 ,在極坐標(biāo)系下,圓C的極坐標(biāo)方程為
,在極坐標(biāo)系下,圓C的極坐標(biāo)方程為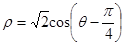 。
。
(1)寫出直線l的參數(shù)方程,并把圓C的方程化為直角坐標(biāo)方程;
(2)設(shè)l與圓C相交于A,B兩點(diǎn),求點(diǎn)P到A,B兩點(diǎn)的距離之積。

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知?jiǎng)狱c(diǎn) ,Q都在曲線C:
,Q都在曲線C: (β為參數(shù))上,對應(yīng)參數(shù)分別為
(β為參數(shù))上,對應(yīng)參數(shù)分別為
與 (0<
(0<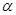 <2π),M為PQ的中點(diǎn)。
<2π),M為PQ的中點(diǎn)。
(Ⅰ)求M的軌跡的參數(shù)方程
(Ⅱ)將M到坐標(biāo)原點(diǎn)的距離d表示為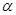 的函數(shù),并判斷M的軌跡是否過坐標(biāo)原點(diǎn)。
的函數(shù),并判斷M的軌跡是否過坐標(biāo)原點(diǎn)。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知點(diǎn)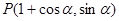 ,參數(shù)
,參數(shù)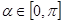
 ,點(diǎn)Q在曲線C:
,點(diǎn)Q在曲線C: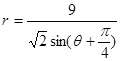 上.
上.
(Ⅰ)求點(diǎn)P的軌跡方程與曲線C的直角坐標(biāo)方程;
(Ⅱ)求點(diǎn)P與點(diǎn)Q之間的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
在直角坐標(biāo)系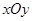 中,曲線
中,曲線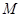 的參數(shù)方程為
的參數(shù)方程為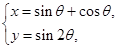 (
(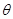 為參數(shù)),若以直角坐標(biāo)系的原點(diǎn)
為參數(shù)),若以直角坐標(biāo)系的原點(diǎn)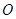 為極點(diǎn),
為極點(diǎn),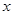 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線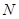 的極坐標(biāo)方程為
的極坐標(biāo)方程為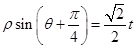 (其中
(其中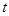 為常數(shù)).
為常數(shù)).
(1)若曲線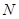 與曲線
與曲線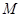 只有一個(gè)公共點(diǎn),求
只有一個(gè)公共點(diǎn),求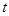 的取值范圍;
的取值范圍;
(2)當(dāng)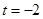 時(shí),求曲線
時(shí),求曲線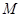 上的點(diǎn)與曲線
上的點(diǎn)與曲線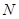 上的點(diǎn)的最小距離.
上的點(diǎn)的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分10分)
在平面直角坐標(biāo)系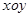 中,直線
中,直線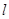 的參數(shù)方程為
的參數(shù)方程為 (t為參數(shù),α為直線
(t為參數(shù),α為直線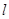 的傾斜角),以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,圓C的極坐標(biāo)方程為
的傾斜角),以原點(diǎn)O為極點(diǎn),x軸的正半軸為極軸建立極坐標(biāo)系,圓C的極坐標(biāo)方程為 .
.
(1) 若直線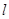 與圓C相切,求
與圓C相切,求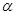 的值;
的值;
(2) 若 直線
直線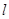 與圓C交與A,B兩點(diǎn),求
與圓C交與A,B兩點(diǎn),求 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知直線l經(jīng)過點(diǎn)P(1,1),傾斜角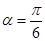 .
.
(1)寫出直線l的參數(shù)方程;
(2)設(shè)l與圓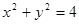 相交于兩點(diǎn)A,B,求點(diǎn)P到A,B兩點(diǎn)的距離之積.
相交于兩點(diǎn)A,B,求點(diǎn)P到A,B兩點(diǎn)的距離之積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
某醫(yī)療研究所為了檢驗(yàn)新開發(fā)的流感疫苗對甲型H1N1流感的預(yù)防作用,把1000名注射了疫苗的人與另外1000名未注射疫苗的人的半年的感冒記錄作比較,提出假設(shè)H0:“這種疫苗不能起到預(yù)防甲型H1N1流感的作用”,并計(jì)算出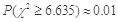 ,則下列說法正確的( )
,則下列說法正確的( )
| A.這種疫苗能起到預(yù)防甲型H1N1流感的有效率為1% |
| B.若某人未使用該疫苗,則他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握認(rèn)為“這種疫苗能起到預(yù)防甲型H1N1流感的作用” |
| D.有99%的把握認(rèn)為“這種疫苗能起到預(yù)防甲型H1N1流感的作用” |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
對四組數(shù)據(jù)進(jìn)行統(tǒng)計(jì),獲得以下散點(diǎn)圖,關(guān)于其相關(guān)系數(shù)的比較,正確的是( ).
| A.r2<r4<0<r3<r1 | B.r4<r2<0<r1<r3 | C.r4<r2<0<r3<r1 | D.r2<r4<0<r1<r3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com