
已知函數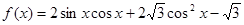 ,
, .
.
(1)求函數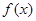 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
(2)在銳角三角形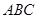 中,若
中,若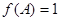 ,
,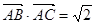 ,求△
,求△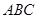 的面積.
的面積.
(1)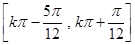 (
(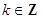 );(2)
);(2)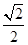 .
.
【解析】
試題分析:(1)三角函數問題一般都是要把三角函數化為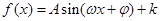 形式,然后利用正弦函數的知識解決問題,本題中選用二倍角公式和降冪公式化簡為
形式,然后利用正弦函數的知識解決問題,本題中選用二倍角公式和降冪公式化簡為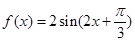 ;(2)三角形的面積公式很多,具體地要選用哪個公式,要根據題意來確定,本題中已知
;(2)三角形的面積公式很多,具體地要選用哪個公式,要根據題意來確定,本題中已知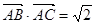 ,而
,而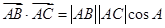 ,因此我們選面積公式
,因此我們選面積公式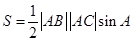 ,正好由已知條件可求出
,正好由已知條件可求出 ,也即求出
,也即求出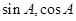 ,從而得面積.
,從而得面積.
試題解析:(1)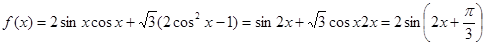 , (2分)
, (2分)
所以,函數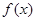 的最小正周期為
的最小正周期為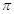 .
(1分)
.
(1分)
由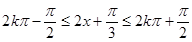 (
(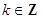 ),
(2分)
),
(2分)
得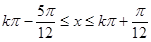 (
(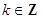 ),
(2分)
),
(2分)
所以,函數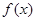 的單調遞增區間是
的單調遞增區間是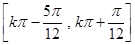 (
(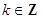 ). (1分)
). (1分)
(2)由已知,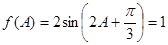 ,所以
,所以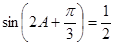 , (1分)
, (1分)
因為 ,所以
,所以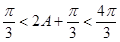 ,所以
,所以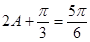 ,從而
,從而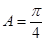 . (2分)
. (2分)
又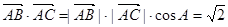 ,,所以,
,,所以,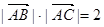 , (1分)
, (1分)
所以,△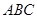 的面積
的面積 . (2分)
. (2分)
考點:(1)三角函數的性質;(2)三角形的面積.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| x |
| 1 |
| n2(n+1)2 |
| 1 |
| 4n |
| 3 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com