設

,證明:
(Ⅰ)當x﹥1時,
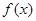
﹤
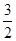
(
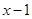
);
(Ⅱ)當
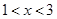
時,

。
(Ⅰ)證法一:記
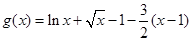
,
則當x>1時,
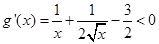
.
又
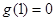
有
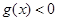
, 即
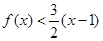
證法二:由均值不等式,當x>1時,
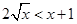
,故
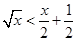
①
令
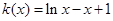
,則
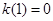
,
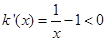
.
故
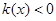
,即
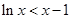
②
由①②得,當x>1時,
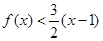
.
(Ⅱ)(證法一)
記
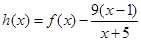
,
由(Ⅰ)得
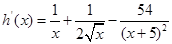
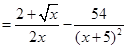
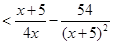

令
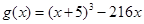
,
則當1<x<3時,
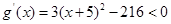
因此
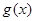
在(1,3)內是遞減函數(shù),
又由
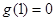
,得
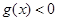
,
所以
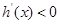
因此
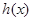
在(1,3)內是遞減函數(shù),
又由
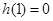
,得
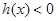
.
于是,當1<x<3時,

(證法二):
記
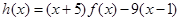
則當1<x<3時,由(Ⅰ)得
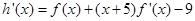
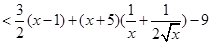

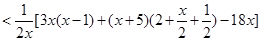
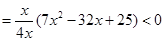
因此
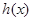
在(1,3)內單調遞減
又
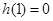
,所以
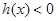
即

.
考點定位:本大題考查導數(shù)題目中較為常規(guī)的類型題目,考查的切線,單調性,以及最值問題都是課本中要求的重點內容,考查構造函數(shù)用求導的方法求最值的能力
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知a、b、u∈R+,且
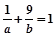
,則使得a+b≥u恒成立的u的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
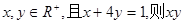
的最大值為
;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
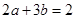
,則
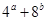
的最小值是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
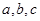
成等比數(shù)列,且
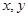
分別為
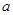
與
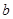
,
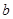
與
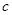
的等差中項,則
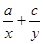
的值為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知
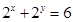
,則
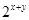
的最大值是
查看答案和解析>>

 ,證明:
,證明: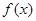 ﹤
﹤ 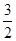 (
( 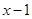 );
);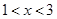 時,
時, 。
。 高中必刷題系列答案
高中必刷題系列答案