
【題目】設函數![]()
(1)若函數![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,求實數
上遞減,求實數![]() 的值.
的值.
(2))討論![]() 在
在![]() 上的單調性;
上的單調性;
(3)若方程![]() 有兩個不等實數根
有兩個不等實數根![]() ,求實數
,求實數![]() 的取值范圍,并證明
的取值范圍,并證明![]() .
.
【答案】(1)![]() (2)見解析(3)
(2)見解析(3)![]() ,見解析
,見解析
【解析】
(1)根據單調區間判斷出![]() 是極值點,由此根據極值點對應的導數值為
是極值點,由此根據極值點對應的導數值為![]() 求解出
求解出![]() 的值,并注意驗證是否滿足;
的值,并注意驗證是否滿足;
(2)先求解出![]() ,然后結合所給區間對
,然后結合所給區間對![]() 進行分類討論,分別求解出
進行分類討論,分別求解出![]() 的單調性;
的單調性;
(3)構造函數![]() ,分析
,分析![]() 的取值情況,由此求解出
的取值情況,由此求解出![]() 的取值范圍;將證明
的取值范圍;將證明![]() 通過條件轉化為證明
通過條件轉化為證明![]() ,由此構造新函數
,由此構造新函數![]() 進行分析證明.
進行分析證明.
(1)由于函數函數![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
由單調性知![]() 是函數的極大值點,無極小值點,所以
是函數的極大值點,無極小值點,所以![]() ,
,
∵![]() ,
,
故![]() ,此時
,此時![]() 滿足
滿足![]() 是極大值點,
是極大值點,
所以![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
①當![]() 時,
時,![]() 在
在![]() 上單調遞增.
上單調遞增.
②當![]() ,即
,即![]() 或
或![]() 時,
時,![]() ,
,
∴![]() 在
在![]() 上單調遞減.
上單調遞減.
③當![]() 且
且![]() 時,
時,
由![]() 得
得![]() .
.
令![]() 得
得![]() ;令
;令![]() 得
得![]() .
.
∴![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上,當![]() 時,
時,![]() 在
在![]() 上遞增;
上遞增;
當![]() 或
或![]() 時,
時,![]() 在
在![]() 上遞減;
上遞減;
當![]() 且
且![]() 時,
時,![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減.
上遞減.
(3)令![]() ,
,![]()
當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增;
單調遞增;
故![]() 在
在![]() 處取得最小值為
處取得最小值為![]()
又當![]() ,由圖象知:
,由圖象知:![]()
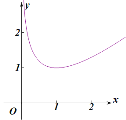
不妨設![]() ,則有
,則有![]() ,
,
![]()
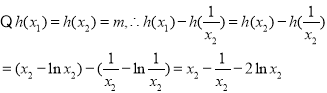
令![]()
![]() 在
在![]() 上單調遞增,故
上單調遞增,故![]()
即![]() ,
,![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】若正整數數列![]() ,
,![]() 滿足:對任意
滿足:對任意![]() ,
,![]() ,都有
,都有![]() 恒成立,則稱數列
恒成立,則稱數列![]() ,
,![]() 為“友好數列”.
為“友好數列”.
(1)已知數列![]() ,
,![]() 的通項公式分別為
的通項公式分別為![]() ,
,![]() ,求證:數列
,求證:數列![]() ,
,![]() 為“友好數列”;
為“友好數列”;
(2)已知數列![]() ,
,![]() 為“友好數列”,且
為“友好數列”,且![]() ,求證:“數列
,求證:“數列![]() 是等差數列” 是“數列
是等差數列” 是“數列![]() 是等比數列”的充分不必要條件.
是等比數列”的充分不必要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的機器上有一種易損元件A,這種元件在使用過程中發生損壞時,需要送維修處維修.工廠規定當日損壞的元件A在次日早上 8:30 之前送到維修處,并要求維修人員當日必須完成所有損壞元件A的維修工作.每個工人獨立維修A元件需要時間相同.維修處記錄了某月從1日到20日每天維修元件A的個數,具體數據如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A個數 | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A個數 | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
從這20天中隨機選取一天,隨機變量X表示在維修處該天元件A的維修個數.
(Ⅰ)求X的分布列與數學期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前維修處有兩名工人從事維修工作,為使每個維修工人每天維修元件A的個數的數學期望不超過4個,至少需要增加幾名維修工人?(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,![]() 垂直于梯形
垂直于梯形![]() 所在的平面,
所在的平面,![]() 為
為![]() 的中點,
的中點,![]() ,四邊形
,四邊形![]() 為矩形,線段
為矩形,線段![]() 交
交![]() 于點
于點![]() .
.
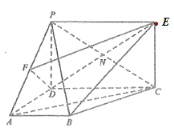
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,設A是由![]() 個實數組成的n行n列的數表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的實數,且aij
個實數組成的n行n列的數表,其中aij (i,j=1,2,3,…,n)表示位于第i行第j列的實數,且aij![]() {1,-1}.記S(n,n)為所有這樣的數表構成的集合.對于
{1,-1}.記S(n,n)為所有這樣的數表構成的集合.對于![]() ,記ri (A)為A的第i行各數之積,cj (A)為A的第j列各數之積.令
,記ri (A)為A的第i行各數之積,cj (A)為A的第j列各數之積.令![]()
a11 | a12 | … | a1n |
a21 | a22 | a2n | |
… | … | … | … |
an1 | an2 | … | ann |
(Ⅰ)請寫出一個A![]() S(4,4),使得l(A)=0;
S(4,4),使得l(A)=0;
(Ⅱ)是否存在A![]() S(9,9),使得l(A)=0?說明理由;
S(9,9),使得l(A)=0?說明理由;
(Ⅲ)給定正整數n,對于所有的A![]() S(n,n),求l(A)的取值集合.
S(n,n),求l(A)的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過點
經過點![]() ,
,![]() ,且圓心在直線
,且圓心在直線![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 截圓所得弦長為
截圓所得弦長為![]() ,求直線
,求直線![]() 的方程.
的方程.
(3)若直線![]() 與圓
與圓![]() 相切,且
相切,且![]() 與
與![]() ,
,![]() 軸的正半軸分別相交于
軸的正半軸分別相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積最小時直線
的面積最小時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com