
【題目】已知函數![]() 是常數.
是常數.
(1)當![]() 時,求函數
時,求函數![]() 的值域;
的值域;
(2)當![]() 時,求方程
時,求方程![]() 的解集;
的解集;
(3)若函數![]() 在區間
在區間![]() 上有零點,求實數
上有零點,求實數![]() 的取值范圍.
的取值范圍.
 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x+ ![]() ,g(x)=2x+a,若x1∈[
,g(x)=2x+a,若x1∈[ ![]() ,3],x2∈[2,3],使得f(x1)≥g(x2),則實數a的取值范圍是( )
,3],x2∈[2,3],使得f(x1)≥g(x2),則實數a的取值范圍是( )
A.a≤1
B.a≥1
C.a≤0
D.a≥0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax﹣lnx;g(x)= ![]() .
.
(1)討論函數f(x)的單調性;
(2)求證:若a=e(e是自然常數),當x∈[1,e]時,f(x)≥e﹣g(x)恒成立;
(3)若h(x)=x2[1+g(x)],當a>1時,對于x1∈[1,e],x0∈[1,e],使f(x1)=h(x0),求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】大衍數列,來源于中國古代著作《乾坤譜》中對易傳“大衍之數五十”的推論.其前10項為:0、2、4、8、12、18、24、32、40、50.通項公式: 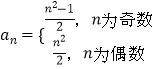 ,如果把這個數列{an}排成如圖形狀,并記A(m,n)表示第m行中從左向右第n個數,則A(10,4)的值為( )
,如果把這個數列{an}排成如圖形狀,并記A(m,n)表示第m行中從左向右第n個數,則A(10,4)的值為( ) 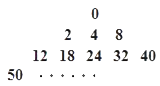
A.1200
B.1280
C.3528
D.3612
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=lnx,g(x)=f(x)+f′(x). (Ⅰ)求g(x)的單調區間和最小值;
(Ⅱ)討論g(x)與 ![]() 的大小關系;
的大小關系;
(Ⅲ)求a的取值范圍,使得g(a)﹣g(x)< ![]() 對任意x>0成立.
對任意x>0成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣1)ex﹣kx2+2,k∈R. (Ⅰ) 當k=0時,求f(x)的極值;
(Ⅱ) 若對于任意的x∈[0,+∞),f(x)≥1恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點O為坐標原點,橢圓E: ![]() (a≥b>0)的右頂點為A,上頂點為B,過點O且斜率為
(a≥b>0)的右頂點為A,上頂點為B,過點O且斜率為 ![]() 的直線與直線AB相交M,且
的直線與直線AB相交M,且 ![]() .
.
(Ⅰ)求橢圓E的離心率e;
(Ⅱ)PQ是圓C:(x﹣2)2+(y﹣1)2=5的一條直徑,若橢圓E經過P,Q兩點,求橢圓E的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.

(1)證明:平面ADB⊥平面BDC;
(2)若BD=1,求三棱錐D-ABC的表面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com