
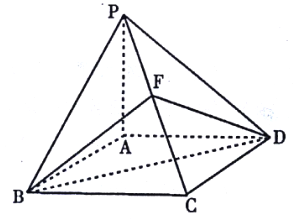
【題目】如圖,已知四棱錐![]() 的底面
的底面![]() 是菱形,
是菱形, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 為
為![]() 的中點.
的中點.
(1)求證: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2) ![]()
【解析】試題分析:
(1)由題意可證得![]() ,結合直線與平面平行的判定定理即可證得
,結合直線與平面平行的判定定理即可證得![]() 平面
平面![]() ;
;
(2)建立空間直角坐標系,結合半平面的法向量可得二面角![]() 的余弦值是
的余弦值是![]()
試題解析:
(1)連結![]() 與
與![]() 交于點
交于點![]() ,連結
,連結![]() .
.
∵![]() 是菱形,∴
是菱形,∴![]() 是
是![]() 的中點,∵點為
的中點,∵點為![]() 的中點,∴
的中點,∴![]() .∵
.∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)∵![]() 是菱形,且
是菱形,且![]() ,∴
,∴![]() 是正三角形.如圖,以點
是正三角形.如圖,以點![]() 為坐標原點,線段
為坐標原點,線段![]() 的垂直平分線所在直線為
的垂直平分線所在直線為![]() 軸,
軸, ![]() 所在直線為
所在直線為![]() 軸,
軸, ![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系,令
軸,建立空間直角坐標系,令![]() ,則
,則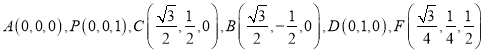 .
.
所以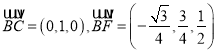 ,設平面
,設平面![]() 的一個法向量為
的一個法向量為![]() ,由
,由![]() ,得
,得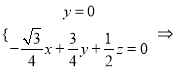
 ,令
,令![]() ,則
,則![]() ,∴
,∴ ,
,
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() 是菱形,∴
是菱形,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
∴![]() 是平面
是平面![]() 的一個法向量,
的一個法向量, 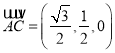 ,∴
,∴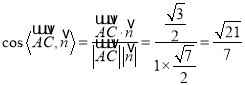 ,
,
∴二面角![]() 的余弦值是
的余弦值是![]() .
.


科目:高中數學 來源: 題型:
【題目】下面程序的功能是( )
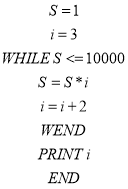
A. 求1×2×3×4×…×10 00的值
B. 求2×4×6×8×…×10 000的值
C. 求3×5×7×9×…×10 001的值
D. 求滿足1×3×5×…×n>10 000的最小正整數n
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)求經過兩直線2x-3y-3=0和x+y+2=0的交點且與直線3x+y-1=0平行的直線l的方程;
(2)求經過兩直線l1:x-2y+4=0和l2:x+y-2=0的交點P,且與直線l3:3x-4y+5=0垂直的直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校為了了解高三學生每天自主學習中國古典文學的時間,隨機抽取了高三男生和女生各50名進行問卷調查,其中每天自主學習中國古典文學的時間超過3小時的學生稱為“古文迷”,否則為“非古文迷”,調查結果如表:
古文迷 | 非古文迷 | 合計 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據表中數據判斷能否有![]() 的把握認為“古文迷”與性別有關?
的把握認為“古文迷”與性別有關?
(2)先從調查的女生中按分層抽樣的方法抽出5人進行理科學習時間的調查,求所抽取的5人中“古文迷”和“非古文迷”的人數;
(3)現從(2)中所抽取的5人中再隨機抽取3人進行體育鍛煉時間的調查,記這3人中“古文迷”的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望.
的分布列與數學期望.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
參考公式: 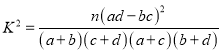 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解甲、乙兩廠的產品質量,采用分層抽樣的方法從甲、乙兩廠生產的產品中分別抽取14件和5件,測量產品中微量元素![]() ,
,![]() 的含量(單位:毫克).下表是乙廠的5件產品的測量數據:
的含量(單位:毫克).下表是乙廠的5件產品的測量數據:
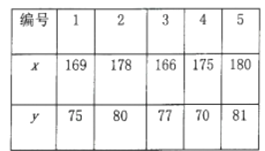
當產品中的微量元素![]() ,
,![]() 滿足
滿足![]() 且
且![]() 時,該產品為優等品
時,該產品為優等品
(1)若甲廠生產的產品共98件,用上述樣本數據估計乙廠生產的優等品的數量;
(2)從乙廠抽出的上述5件產品中,隨機抽取2件,求抽取的2件產品中優等品數![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙二人同時從![]() 地趕住
地趕住![]() 地,甲先騎自行車到兩地的中點再改為跑步;乙先跑步到兩地的中點再改為騎自行車,最后兩人同時到達
地,甲先騎自行車到兩地的中點再改為跑步;乙先跑步到兩地的中點再改為騎自行車,最后兩人同時到達![]() 地.已知甲騎自行車比乙騎自行車的速度快,且兩人騎車的速度均大于跑步的速度.現將兩人離開
地.已知甲騎自行車比乙騎自行車的速度快,且兩人騎車的速度均大于跑步的速度.現將兩人離開![]() 地的距離
地的距離![]() 與所用時間
與所用時間![]() 的函數關系用圖象表示如下:
的函數關系用圖象表示如下:

則上述四個函數圖象中,甲、乙兩人運行的函數關系的圖象應該分別是( )
A. 圖①、圖② B. 圖①、圖④ C. 圖③、圖② D. 圖③、圖④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() .對于
.對于![]() ,
, ![]() ,定義
,定義![]() 與
與![]() 之間的距離為
之間的距離為![]() .
.
(Ⅰ)寫出![]() 中的所有元素,并求兩元素間的距離的最大值;
中的所有元素,并求兩元素間的距離的最大值;
(Ⅱ)若集合![]() 滿足:
滿足: ![]() ,且任意兩元素間的距離均為2,求集合
,且任意兩元素間的距離均為2,求集合![]() 中元素個數的最大值并寫出此時的集合
中元素個數的最大值并寫出此時的集合![]() ;
;
(Ⅲ)設集合![]() ,
, ![]() 中有
中有![]() 個元素,記
個元素,記![]() 中所有兩元素間的距離的平均值為
中所有兩元素間的距離的平均值為![]() ,證明
,證明![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點,以
兩點,以![]() 為對角線作正方形
為對角線作正方形![]() ,記直線
,記直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,問
,問![]() 、
、![]() 兩點間距離是否為定值?如果是,求出定值;如果不是,請說明理由.
兩點間距離是否為定值?如果是,求出定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省電視臺為了解該省衛視一檔成語類節目的收視情況,抽查東西兩部各個城市,得到觀看該節目的人數(單位:千人),如莖葉圖所示,其中一個數字被污損.
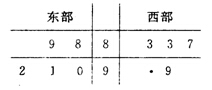
(1)求東部各城市觀看該節目觀眾平均人數超過西部各城市觀看該節目觀眾平均人數的概率;
(2)隨著節目的播出,極大激發了觀眾對成語知識學習積累的熱情,從中獲益匪淺.現從觀看該節目的觀眾中隨機統計了位觀眾的周均學習成語知識的時間(單位:小時)與年齡(單位:歲),并制作了對照表(如下表所示),
年齡x(歲) | ||||
周均學習成語知識時間y(小時) |
由表中數據,試求線性回歸方程,并預測年齡為歲觀眾周均學習成語知識時間.
參考公式: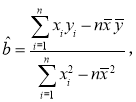 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com