

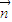 ,又
,又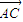 =(0,2m,0)是平面BDD1的一個法向量,則cosθ=
=(0,2m,0)是平面BDD1的一個法向量,則cosθ=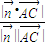 ,利用向量的數(shù)量積運算表示出來,然后借助函數(shù)的性質(zhì)即可求得其范圍;
,利用向量的數(shù)量積運算表示出來,然后借助函數(shù)的性質(zhì)即可求得其范圍;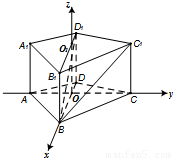
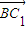 =(-n,m,1),
=(-n,m,1),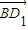 =(-2n,0,1),
=(-2n,0,1),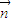 =(x,y,z)是平面BC1D1的一個法向量,
=(x,y,z)是平面BC1D1的一個法向量,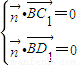 得
得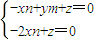 ,令x=m,則y=-n,z=2mn,
,令x=m,則y=-n,z=2mn,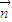 =(m,-n,2mn),
=(m,-n,2mn),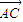 =(0,2m,0)是平面BDD1的一個法向量,
=(0,2m,0)是平面BDD1的一個法向量,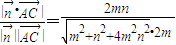 =
=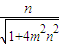 =
= ,
,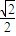 ,則0<t<
,則0<t< ,cosθ=
,cosθ=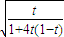 =
=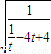 ,
, -4t在(0,
-4t在(0, )上單調(diào)遞減,∴y=
)上單調(diào)遞減,∴y=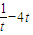 >0,
>0, ,
,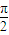 ,∴
,∴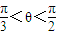 ,即平面BDD1與平面BC1D1所成角的取值范圍為(
,即平面BDD1與平面BC1D1所成角的取值范圍為(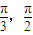 ).
).

 步步高達標卷系列答案
步步高達標卷系列答案科目:高中數(shù)學 來源: 題型:
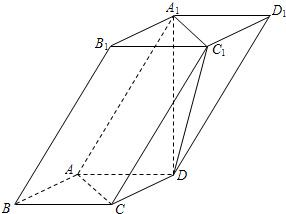 如圖,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是邊長為1的正方形,側(cè)棱AA1=2.
如圖,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是邊長為1的正方形,側(cè)棱AA1=2.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
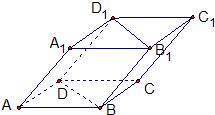 如圖,四棱柱ABCD-A1B1C1D1的底面ABCD為正方形,側(cè)棱與底面邊長均為2a,且∠A1AD=∠A1AB=60°,則側(cè)棱AA1和截面B1D1DB的距離是
如圖,四棱柱ABCD-A1B1C1D1的底面ABCD為正方形,側(cè)棱與底面邊長均為2a,且∠A1AD=∠A1AB=60°,則側(cè)棱AA1和截面B1D1DB的距離是查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
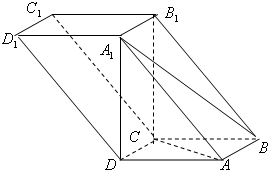 如圖,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是邊長為1的正方形,側(cè)棱A1A=2,
如圖,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是邊長為1的正方形,側(cè)棱A1A=2,| AP |
| PA1 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (2013•泉州模擬)如圖,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.
(2013•泉州模擬)如圖,四棱柱ABCD-A1B1C1D1中,AA1⊥平面ABCD.查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (2013•天津)如圖,四棱柱ABCD-A1B1C1D1中,側(cè)棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
(2013•天津)如圖,四棱柱ABCD-A1B1C1D1中,側(cè)棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,
| ||
| 6 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com