
【題目】已知函數![]()
![]() ,其中
,其中![]() .
.
(Ⅰ)討論![]() 的單調性;
的單調性;
(Ⅱ)若存在![]() 使得
使得![]() ,求實數
,求實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)若當![]() 時恒有
時恒有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)見解析.(Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]() .
.
【解析】試題分析:(Ⅰ)求得函數的導數![]() ,得到
,得到![]() 的根,分類討論,即可求解函數的單調區間;
的根,分類討論,即可求解函數的單調區間;
(Ⅱ)令![]() ,轉化為
,轉化為![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,又由
上有解,又由![]() 關于
關于![]() 單調遞增,求得實數
單調遞增,求得實數![]() 的取值范圍;
的取值范圍;
(Ⅲ)由題意,得到![]() ,取得
,取得![]() ,得得
,得得![]() ,由(Ⅱ)知,分類討論即可求解實數
,由(Ⅱ)知,分類討論即可求解實數![]() 的取值范圍.
的取值范圍.
試題解析:
(Ⅰ)![]()
![]()
![]() .
.
令![]() 得
得![]() 或
或![]() .
.
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,令
時,令![]() 得
得![]() 或
或![]() ,從而
,從而![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(Ⅱ)![]()
![]() ,令
,令![]() ,
,
則![]()
![]() ,當且僅當
,當且僅當![]() 取得等號.
取得等號.
注意到![]()
![]() ,
,
原問題轉化為![]() 在
在![]() 上有解,即
上有解,即![]() 在
在![]() 上有解,又
上有解,又![]() 關于
關于![]() 單調遞增,從而
單調遞增,從而![]() ,
,
又![]() ,綜合得
,綜合得![]() .
.
(Ⅲ)令![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
得![]() ,由(Ⅱ)知
,由(Ⅱ)知![]() .
.
當![]() ,即
,即![]() 時,
時,![]() ,又
,又![]() ,從而當
,從而當![]() 時恒有
時恒有![]() ,
,
當![]() 時,存在
時,存在![]() 使得
使得![]() ,即
,即![]() ,即
,即![]() ,
,
解得![]() ,
,![]() ,(
,(![]() 舍去).
舍去).
從而當![]() 時
時![]() ,此時
,此時![]() ,矛盾.
,矛盾.
綜上![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且
,且![]() 過點
過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(點
兩點(點![]() 均在第一象限),
均在第一象限),![]() 與
與![]() 軸,
軸,![]() 軸分別交于
軸分別交于![]() 兩點,且滿足
兩點,且滿足![]() (其中
(其中![]() 為坐標原點).證明:直線
為坐標原點).證明:直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1)若A∩B=[0,3],求實數m的值;
(2)若ARB,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 的通項公式是
的通項公式是![]() (
(![]() 表示不超過實數
表示不超過實數![]() 的最大整數).
的最大整數).
(1)證明:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 都是數列
都是數列![]() 的項;
的項;
(2)![]() 是否是數列
是否是數列![]() 的項,證明你的結論;
的項,證明你的結論;
(3)證明:有無窮多個2的正整數冪是數列![]() 的項.
的項.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一種候鳥每年都按一定的路線遷徙,飛往繁殖地產卵,科學家經過測量發現候鳥的飛行速度可以表示為函數![]() ,單位是
,單位是![]() ,其中
,其中![]() 表示候鳥每分鐘耗氧量的單位數,
表示候鳥每分鐘耗氧量的單位數,![]() 為表示測量過程中候鳥每分鐘的耗氧偏差.(參考數據:
為表示測量過程中候鳥每分鐘的耗氧偏差.(參考數據:![]() ,
,![]() ,
,![]() )
)
(1)若![]() ,候鳥停下休息時,它每分鐘的耗氧量為多少個單位?
,候鳥停下休息時,它每分鐘的耗氧量為多少個單位?
(2)若雄鳥的飛行速度為![]() ,雌鳥的飛行速度為
,雌鳥的飛行速度為![]() ,那么此時雄鳥每分鐘的耗氧量是雌鳥每分鐘耗氧量的多少倍?
,那么此時雄鳥每分鐘的耗氧量是雌鳥每分鐘耗氧量的多少倍?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且經過點
,且經過點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為橢圓的四個頂點(如圖),直線
為橢圓的四個頂點(如圖),直線![]() 過右頂點
過右頂點![]() 且垂直于
且垂直于![]() 軸.
軸.
(1)求該橢圓的標準方程;
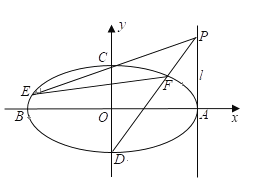
(2)![]() 為
為![]() 上一點(
上一點(![]() 軸上方),直線
軸上方),直線![]() ,
,![]() 分別交橢圓于
分別交橢圓于![]() ,
,![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() 為自然對數的底數)
為自然對數的底數)
(1)判斷函數![]() 的單調性并證明;
的單調性并證明;
(2)判斷函數![]() 的奇偶性并證明;
的奇偶性并證明;
(3)是否存在實數![]() ,使不等式
,使不等式![]() 對一切
對一切![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的范圍,若不存在說明理由.
的范圍,若不存在說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com