
 +
+ +c≥0的解集為[0,22],則使數(shù)列{an}的前n項和Sn最大的正整數(shù)n的值是 .
+c≥0的解集為[0,22],則使數(shù)列{an}的前n項和Sn最大的正整數(shù)n的值是 . 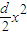 +
+ +c≥0的解集為[0,22],我們根據(jù)不等式解析的形式及韋達(dá)定理,易判斷出數(shù)列的首項為正,公差為負(fù),及首項與公差之間的比例關(guān)系,進(jìn)而判斷出數(shù)列項的符號變化分界點,即可得到答案.
+c≥0的解集為[0,22],我們根據(jù)不等式解析的形式及韋達(dá)定理,易判斷出數(shù)列的首項為正,公差為負(fù),及首項與公差之間的比例關(guān)系,進(jìn)而判斷出數(shù)列項的符號變化分界點,即可得到答案.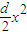 +
+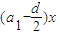 +c≥0的解集為[0,22],
+c≥0的解集為[0,22],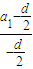 ,且
,且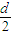 >0
>0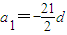 >0,
>0,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| 1 |
| an |
| pn+q |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com