
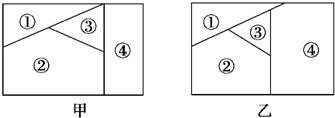
 用n種不同顏色為下側兩塊廣告牌著色(如圖甲、乙所示),要求在①、②、③、④四個區域中相鄰(有公共邊界)的區域不用同一種顏色.
用n種不同顏色為下側兩塊廣告牌著色(如圖甲、乙所示),要求在①、②、③、④四個區域中相鄰(有公共邊界)的區域不用同一種顏色.

科目:高中數學 來源: 題型:
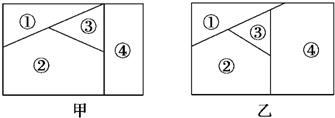 18、用n種不同顏色為下側兩塊廣告牌著色(如圖甲、乙所示),要求在①、②、③、④四個區域中相鄰(有公共邊界)的區域不用同一種顏色.
18、用n種不同顏色為下側兩塊廣告牌著色(如圖甲、乙所示),要求在①、②、③、④四個區域中相鄰(有公共邊界)的區域不用同一種顏色.查看答案和解析>>
科目:高中數學 來源:2011年高三數學第一輪復習鞏固與練習:計數原理(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com