
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,證明:
時,證明: ![]() ;
;
(Ⅱ)當![]() ,且
,且![]() 時,不等式
時,不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍 .
的取值范圍 .
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)要證![]() ,只需證
,只需證![]() ,構造差函數
,構造差函數![]() ,轉化為證明
,轉化為證明![]() 最小值大于零,利用導數研究函數
最小值大于零,利用導數研究函數![]() 單調性,可得結果,(2)先化簡所求不等式:
單調性,可得結果,(2)先化簡所求不等式:  ,分
,分![]() 及
及![]() 兩種情況說明,主要研究分子函數
兩種情況說明,主要研究分子函數![]() ,利用二次求導可得當
,利用二次求導可得當![]() 時,
時, ![]() 在
在![]() 上是減函數,
上是減函數, ![]() 在
在![]() 上是減函數,
上是減函數, ![]() ;
; ![]() 在
在![]() 上是增函數,
上是增函數, ![]() 在
在![]() 上是減函數,從而,
上是減函數,從而, ![]() ,因此當
,因此當![]() 時,滿足題意.
時,滿足題意.
試題解析:(Ⅰ)證明:∵![]() ,
, ![]() ,
, ![]() ,即
,即![]() ,
,
令![]() ,
, 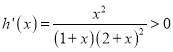 ,則
,則![]() 在
在![]() 上是增函數,
上是增函數,
故![]() ,即命題結論成立.
,即命題結論成立.
(Ⅱ)原不等式等價于![]() .
.
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
,
原不等式等價于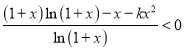 ,
,
令![]() ,
,
令![]() ,
, ![]() ,
,
①當![]() 時,有
時,有![]() ,
,
令![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是減函數,即
上是減函數,即![]() ,
,
因此![]() 在
在![]() 上是減函數,從而
上是減函數,從而![]() ,
,
所以,當![]() 時,對于
時,對于![]() ,有
,有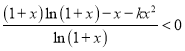 ,
,
當![]() 時,有
時,有![]() ,
,
令![]() ,則
,則![]() ,故
,故![]() 在
在![]() 上是增函數,即
上是增函數,即![]() ,
,
因此, ![]() 在
在![]() 上是減函數,從而,
上是減函數,從而, ![]() ,
,
所以當![]() 時,對于
時,對于![]() ,有
,有 ,
,
綜上,當![]() 時,在
時,在![]() ,且
,且![]() 時,不等式
時,不等式![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】在等比數列{an}中,公比q≠1,等差數列{bn}滿足b1=a1=3,b4=a2 , b13=a3 .
(1)求數列{an}與{bn}的通項公式;
(2)記cn=(﹣1)nbn+an , 求數列{cn}的前n項和Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了解高中入學新生的身高情況,從高一年級學生中按分層抽樣共抽取了50名學生的身高數據,分組統計后得到了這50名學生身高的頻數分布表:

(Ⅰ)在答題卡上作出這50名學生身高的頻率分布直方圖;
(Ⅱ)估計這50名學生身高的方差(同一組中的數據用該組區間的中點值作代表);
(Ⅲ)現從身高在![]() 這6名學生中隨機抽取3名,求至少抽到1名女生的概率.
這6名學生中隨機抽取3名,求至少抽到1名女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到定點
到定點![]() 和定直線
和定直線![]() 的距離之比為
的距離之比為![]() ,設動點
,設動點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)過點![]() 作斜率不為0的任意一條直線與曲線
作斜率不為0的任意一條直線與曲線![]() 交于兩點
交于兩點![]() ,試問在
,試問在![]() 軸上是否存在一點
軸上是否存在一點![]() (與點
(與點![]() 不重合),使得
不重合),使得![]() ,若存在,求出
,若存在,求出![]() 點坐標;若不存在,說明理由.
點坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() 為自然對數的底數.
為自然對數的底數.
(1)函數![]() 的圖象能否與
的圖象能否與![]() 軸相切?若能與
軸相切?若能與![]() 軸相切,求實數
軸相切,求實數![]() 的值;否則,請說明理由;
的值;否則,請說明理由;
(2)若函數![]() 在
在![]() 上單調遞增,求實數
上單調遞增,求實數![]() 能取到的最大整數值.
能取到的最大整數值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com