
(本題滿分12分)設函數f(x)=x3- ax2+3x+5(a>0).
ax2+3x+5(a>0).
(1)已知f(x)在R上是單調函數,求a的取值范圍;
(2)若a=2,且當x∈[1,2]時,f(x)≤m恒成立,求實數m的取值范圍.
(1) 0<a≤6 ;(2) [15,+∞).
【解析】
試題分析:(1)f′(x)=3x2-ax+3, 2分
其判別式Δ=a2-36.
當0<a≤6時,f′(x)≥0恒成立, 4分
此時f(x)在R上為增函數. 6分
(2)a=2時,f′(x)=3x2-2x+3>0恒成立,
因此f(x)在(-∞,+∞)上是增函數, 8分
從而f(x)在[1,2]上遞增,則f(x)max=f(2)=15, 10分
要使f(x)≤m在x∈[1,2]上恒成立,只需15≤m,
解得m∈[15,+∞).
故m的取值范圍是[15,+∞). 12分
考點:利用導數研究函數的單調性。
點評:解決恒成立問題常用變量分離法,變量分離法主要通過兩個基本思想解決恒成立問題, 思路1: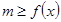 在
在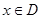 上恒成立
上恒成立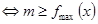 ;思路2:
;思路2: 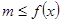 在
在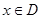 上恒成立
上恒成立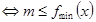 。
。


科目:高中數學 來源:2014屆吉林省吉林市高二上學期期中理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
設命題 :實數
:實數 滿足
滿足 , 命題
, 命題 :實數
:實數 滿足
滿足 .
.
當 為真,求實數
為真,求實數 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源:2012-2013學年河北省石家莊市高三暑期第二次考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)設函數 .
.
(1)求函數 的單調區間;
的單調區間;
(2)若 對
對 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖北省高三十一月份階段性考試理科數學 題型:解答題
(本題滿分12分)設函數 ,其中
,其中 。
。
(Ⅰ)當 時,求不等式
時,求不等式 的解集;
的解集;
(Ⅱ)若不等式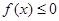 的解集為
的解集為 ,求a的值。
,求a的值。
查看答案和解析>>
科目:高中數學 來源:2010-2011年云南省高二上學期期末數學理卷 題型:解答題
(本題滿分12分)
設 ,
, 分別是橢圓
分別是橢圓 :
: 的左、右焦點,過
的左、右焦點,過 斜率為1的直線
斜率為1的直線 與
與 相交于
相交于 、
、 兩點,且
兩點,且 ,
, ,
, 成等差數列,
成等差數列,
(Ⅰ)求 的離心率;
的離心率;
(Ⅱ)設點 滿足
滿足 ,求
,求 的方程。
的方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com