
【題目】已知![]() ,函數
,函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最值;
上的最值;
(2)若函數![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析;(2)a≥![]() .
.
【解析】
(1) 當a=2時,求得函數的導數,利用導數得出函數的單調性,即可求解函數的最值;
(2)根據函數f(x)在(-1,1)上單調遞增,轉化為![]() 在(-1,1)上恒成立,再利用分離參數,轉化為函數的最值問題,即可求解.
在(-1,1)上恒成立,再利用分離參數,轉化為函數的最值問題,即可求解.
(1) 當a=2時,f(x)=(-x2+2x)ex,f′(x)=(-x2+2)ex.
令f′(x)=0,則x=-![]() 或x=
或x=![]()
當x變化時,f′(x),f(x)的變化情況如下表:
x | 0 | (0, |
| ( | 2 |
f′(x) | + | 0 | - | ||
f(x) | f(0)=0 | ↗ | 極大值f( | ↘ | f(2)=0 |
所以,f(x)max= f(![]() )=(-2+2
)=(-2+2![]() )
)![]() ,f(x)min= f(0)=0.
,f(x)min= f(0)=0.
(2)因為函數f(x)在(-1,1)上單調遞增,所以f′(x)≥0在(-1,1)上恒成立.
又f′(x)=[-x2+(a-2)x+a]ex,即[-x2+(a-2)x+a]ex≥0,注意到ex>0,
因此-x2+(a-2)x+a≥0在(-1,1)上恒成立,
也就是a≥![]() =x+1-
=x+1-![]() 在(-1,1)上恒成立.
在(-1,1)上恒成立.
設y=x+1-![]() ,則y′=1+
,則y′=1+![]() >0,
>0,
即y=x+1-![]() 在(-1,1)上單調遞增,
在(-1,1)上單調遞增,
則y<1+1-![]() =
=![]() ,故a≥
,故a≥![]() .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,圓
中,圓![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() 為平面內一動點,若以線段
為平面內一動點,若以線段![]() 為直徑的圓與圓
為直徑的圓與圓![]() 相切.
相切.
(1)證明![]() 為定值,并寫出點
為定值,并寫出點![]() 的軌跡方程;
的軌跡方程;
(2)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 過
過![]() 交
交![]() 于
于![]() ,
,![]() 兩點,過
兩點,過![]() 且與
且與![]() 垂直的直線與
垂直的直線與![]() 交于
交于![]() ,
,![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,且
,且![]() ).
).
(Ⅰ)求函數![]() 的單調區間;
的單調區間;
(Ⅱ)求函數![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(Ⅰ)![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .(Ⅱ)當
.(Ⅱ)當![]() 時,
時, ![]()
![]() ;當
;當![]() 時,
時, ![]()
![]() .
.
【解析】【試題分析】(I)利用![]() 的二階導數來研究求得函數
的二階導數來研究求得函數![]() 的單調區間.(II) 由(Ⅰ)得
的單調區間.(II) 由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,由此可知
上單調遞增,由此可知![]() .利用導數和對
.利用導數和對![]() 分類討論求得函數在
分類討論求得函數在![]() 不同取值時的最大值.
不同取值時的最大值.
【試題解析】
(Ⅰ)![]() ,
,
設![]()
![]() ,則
,則![]() .
.
∵![]() ,
, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增,
上單調遞增,
從而得![]() 在
在![]() 上單調遞增,又∵
上單調遞增,又∵![]() ,
,
∴當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
因此, ![]() 的單調增區間為
的單調增區間為![]() ,單調減區間為
,單調減區間為![]() .
.
(Ⅱ)由(Ⅰ)得![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
由此可知![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
設![]() ,
,
則![]()
![]()
 .
.
∵當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
又∵![]() ,∴當
,∴當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() .
.
①當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() ;
;
②當![]() 時,
時, ![]() ,即
,即![]() ,這時,
,這時, ![]()
![]() .
.
綜上, ![]() 在
在![]() 上的最大值為:當
上的最大值為:當![]() 時,
時, ![]()
![]() ;
;
當![]() 時,
時, ![]()
![]() .
.
[點睛]本小題主要考查函數的單調性,考查利用導數求最大值. 與函數零點有關的參數范圍問題,往往利用導數研究函數的單調區間和極值點,并結合特殊點,從而判斷函數的大致圖像,討論其圖象與![]() 軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
軸的位置關系,進而確定參數的取值范圍;或通過對方程等價變形轉化為兩個函數圖象的交點問題.
【題型】解答題
【結束】
22
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,圓
中,圓![]() 的普通方程為
的普通方程為![]() . 在以坐標原點為極點,
. 在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ) 寫出圓 ![]() 的參數方程和直線
的參數方程和直線![]() 的直角坐標方程;
的直角坐標方程;
( Ⅱ ) 設直線![]() 與
與![]() 軸和
軸和![]() 軸的交點分別為
軸的交點分別為![]() ,
,![]() 為圓
為圓![]() 上的任意一點,求
上的任意一點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一個總體的100個個體編號為0,1,2,…,99,并依次將其分為10個組,組號為0,1,2,…,9.要用系統抽樣法抽取一個容量為10的樣本,如果在第0組(號碼為0—9)隨機抽取的號碼為2,則抽取的10個號碼為______________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為建立健全國家學生體質健康監測評價機制,激勵學生積極參加身體鍛煉,教育部印發《國家學生體質健康標準(2014年修訂)》,要求各學校每學期開展覆蓋本校各年級學生的《標準》測試工作,并根據學生每個學期總分評定等級.某校決定針對高中學生,每學期進行一次體質健康測試,以下是小明同學六個學期體質健康測試的總分情況.
學期 | 1 | 2 | 3 | 4 | 5 | 6 |
總分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)請根據上表提供的數據,用相關系數![]() 說明
說明![]() 與
與![]() 的線性相關程度,并用最小二乘法求出
的線性相關程度,并用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程(線性相關系數保留兩位小數);
的線性回歸方程(線性相關系數保留兩位小數);
(2)在第六個學期測試中學校根據 《標準》,劃定540分以上為優秀等級,已知小明所在的學習小組10個同學有6個被評定為優秀,測試后同學們都知道了自己的總分但不知道別人的總分,小明隨機的給小組內4個同學打電話詢問對方成績,優秀的同學有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
參考公式: 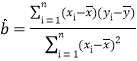 ,
,![]() ;
;
相關系數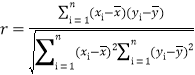 ;
;
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=![]() ,其中2<m<2,m∈Z,滿足:
,其中2<m<2,m∈Z,滿足:
(1)f(x)是區間(0,+∞)上的增函數;
(2)對任意的x∈R,都有f(x) +f(x)=0.
求同時滿足條件(1)、(2)的冪函數f(x)的解析式,并求x∈[0,3]時,f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中心在原點,焦點在![]() 軸上的橢圓,下頂點
軸上的橢圓,下頂點![]() ,且離心率
,且離心率![]() .
.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)經過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點.在
兩點.在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得
,使得![]() 恒成立?若存在,求出點
恒成立?若存在,求出點![]() 坐標;若不存在,說明理由.
坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假定小麥基本苗數![]() 與成熟期有效穗
與成熟期有效穗![]() 之間存在相關關系,今測得5組數據如下:
之間存在相關關系,今測得5組數據如下:

(1)以![]() 為解釋變量,
為解釋變量,![]() 為預報變量,畫出散點圖
為預報變量,畫出散點圖
(2)求![]() 與
與![]() 之間的回歸方程
之間的回歸方程
(3)當基本苗數為![]() 時預報有效穗(注:
時預報有效穗(注: ,
, ![]() )
)![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com