
以下莖葉圖記錄了甲,乙兩組各三名同學在期末考試中的數學成績(滿分為100分).乙組記錄中有一個數字模糊,無法確認,假設這個數字具有隨機性,并在圖中以a表示.
(1)若甲,乙兩個小組的數學平均成績相同,求a的值.
(2)求乙組平均成績超過甲組平均成績的概率.
(3)當a=2時,分別從甲,乙兩組同學中各隨機選取一名同學,求這兩名同學的數學成績之差的絕對值為2分的概率.
(1) ;(2)乙組平均成績超過甲組平均成績的概率為
;(2)乙組平均成績超過甲組平均成績的概率為 ;(3)這兩名同學的數學成績之差的絕對值為2分的概率為
;(3)這兩名同學的數學成績之差的絕對值為2分的概率為 .
.
解析試題分析:(1)甲,乙兩個小組的數學平均成績相同,直接列等式,即可求a的值;
(2)依題意  ,共有10種可能,乙組平均成績超過甲組平均成績,共有8種可能.
,共有10種可能,乙組平均成績超過甲組平均成績,共有8種可能.
所以乙組平均成績超過甲組平均成績的概率 .
.
當 時,分別從甲、乙兩組同學中各隨機選取一名同學,所有可能的成績結果有
時,分別從甲、乙兩組同學中各隨機選取一名同學,所有可能的成績結果有 種, 這兩名同學的數學成績之差的絕對值為2 分的有三種 ,所以這兩名同學的數學成績之差的絕對值為2分的概率P=
種, 這兩名同學的數學成績之差的絕對值為2 分的有三種 ,所以這兩名同學的數學成績之差的絕對值為2分的概率P= .
.
(1)依題意,得  ,解得
,解得  3分
3分
(2)解:設“乙組平均成績超過甲組平均成績”為事件 ,
,
依題意  ,共有10種可能.
,共有10種可能.
由(Ⅰ)可知,當 時甲、乙兩個小組的數學平均成績相同,
時甲、乙兩個小組的數學平均成績相同,
所以當 時,乙組平均成績超過甲組平均成績,共有8種可能.
時,乙組平均成績超過甲組平均成績,共有8種可能.
所以乙組平均成績超過甲組平均成績的概率 . 6分
. 6分
(3)解:當 時,分別從甲、乙兩組同學中各隨機選取一名同學,所有可能的成績結果有
時,分別從甲、乙兩組同學中各隨機選取一名同學,所有可能的成績結果有 種, 它們是:
種, 它們是: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,這兩名同學的數學成績之差的絕對值為2 分的有三種
,這兩名同學的數學成績之差的絕對值為2 分的有三種 

 所以這兩名同學的數學成績之差的絕對值為2分的概率P=
所以這兩名同學的數學成績之差的絕對值為2分的概率P= 9分
9分
考點:概率與統計.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
某大學餐飲中心為了了解新生的飲食習慣,在全校一年級學生中進行了抽樣調查,調查結果如下表所示: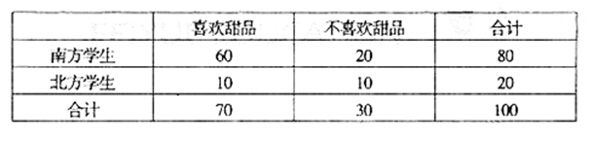
(1)根據表中數據,問是否有95%的把握認為“南方學生和北方學生在選用甜品的飲食習慣方面有差異”;
(2)已知在被調查的北方學生中有5名數學系的學生,其中2名喜歡甜品,現在從這5名學生中隨機抽取3人,求至多有1人喜歡甜品的概率.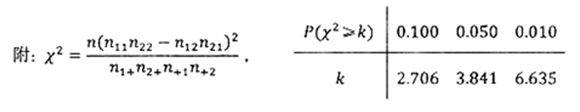
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
由某種設備的使用年限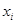 (年)與所支出的維修費
(年)與所支出的維修費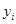 (萬元)的數據資料算得如下結果,
(萬元)的數據資料算得如下結果,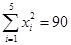 ,
,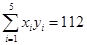 ,
,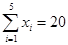 ,
,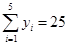 .
.
(1)求所支出的維修費y對使用年限x的線性回歸方程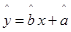 ;
;
(2)①判斷變量x與y之間是正相關還是負相關;
②當使用年限為8年時,試估計支出的維修費是多少.
(附:在線性回歸方程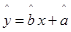 中,)
中,)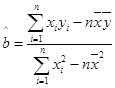 ,
,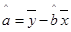 ,其中
,其中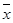 ,
, 為樣本平均值.)
為樣本平均值.)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區間是:[50,60][60,70][70,80][80,90][90,100].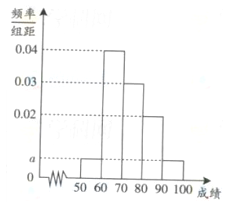
(1)求圖中a的值;
(2)根據頻率分布直方圖,估計這100名學生語文成績的平均分;
(3)若這100名學生語文成績某些分數段的人數(x)與數學成績相應分數段的人數(y)之比如下表所示,求數學成績在[50,90)之外的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為預防X病毒爆發,某生物技術公司研制出一種X病毒疫苗,為測試該疫苗的有效性(若疫苗有效的概率小于90%,則認為測試沒有通過),公司選定2000個樣本分成三組,測試結果如下表:
| 分組 |  組 組 | 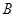 組 組 |  組 組 |
| 疫苗有效 | 673 | 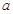 | 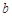 |
| 疫苗無效 | 77 | 90 | 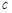 |
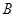 組疫苗有效的概率是0.33.
組疫苗有效的概率是0.33. 組抽取樣本多少個?
組抽取樣本多少個?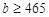 ,
,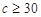 ,求通過測試的概率.
,求通過測試的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高一某班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的破壞,其可見部分如下,據此解答如下問題:


(1)計算頻率分布直方圖中[80,90)間的矩形的高;
(2)若要從分數在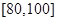 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份的分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份的分數在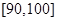 之間的概率;
之間的概率;
(3)根據頻率分布直方圖估計這次測試的平均分.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校為了選拔學生參加“XX市中學生知識競賽”,先在本校進行選拔測試(滿分150分),若該校有100名學生參加選拔測試,并根據選拔測試成績作出如圖所示的頻率分布直方圖.
(1)根據頻率分布直方圖,估算這100名學生參加選拔測試的平均成績;
(2)該校推薦選拔測試成績在110以上的學生代表學校參加市知識競賽,為了了解情況,在該校推薦參加市知識競賽的學生中隨機抽取2人,求選取的兩人的選拔成績在頻率分布直方圖中處于不同組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某企業有兩個分廠生產某種零件,按規定內徑尺寸(單位:mm)的值落在[29.94,30.06)的零件為優質品.從兩個分廠生產的零件中各抽出了500件,量其內徑尺寸,得結果如下表:
甲廠:
| 分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 頻數 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
| 分組 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.9830.02), | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
| 頻數 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
| | 甲廠 | 乙廠 | 合計 |
| 優質品 | | | |
| 非優質品 | | | |
| 合 計 | | | |
| P(χ2≥x0) | 0.05 | 0.01 |
| x0 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關.現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,在將兩組工人的日平均生產件數分成5組: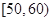 ,
,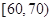 ,
, ,
,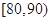 ,
,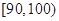 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.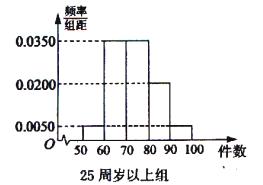
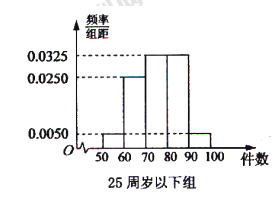

(1)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的頻率.
(2)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成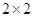 的列聯表,并判斷是否有
的列聯表,并判斷是否有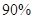 的把握認為“生產能手與工人所在的年齡組有關”?
的把握認為“生產能手與工人所在的年齡組有關”?
附表: 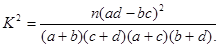
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com