
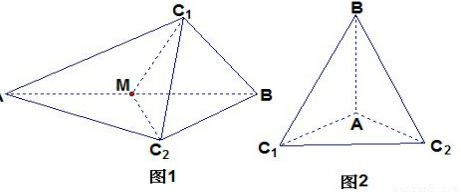
 解:如圖所示,有兩種情況:
解:如圖所示,有兩種情況: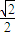
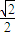
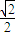 或1.
或1.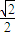 或1.
或1.

科目:高中數學 來源:數學教研室 題型:022
查看答案和解析>>
科目:高中數學 來源:2010屆廣東華南師范大學附屬中學高三模擬數學試題(三) 題型:填空題
兩個腰長均為 1 的等腰直角△ABC1和△ABC2所在的平面構成60°的二面角,則點C1和C2之間的距離等于 。(請寫出所有可能的值)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com