已知sinαcosβ=1,則sin(α-β)= .
【答案】
分析:由sinαcosβ=1得到sinα=cosβ=1或sinα=cosβ=-1,根據同角三角函數間的基本關系分別求出cosα和sinβ,而sin(α-β)=sinαcosβ-cosαsinβ,代入求出值即可.
解答:解:因為-1≤sinα≤1,-1≤cosβ≤1,sinαcosβ=1,得到sinα=cosβ=1或sinα=cosβ=-1;
根據同角三角函數間的基本關系得:cosα=±
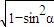
=
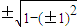
=0,sinβ=
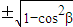
=
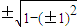
=0;
所以sin(α-β)=sinαcosβ-cosαsinβ=1-0=1.
故答案為:1
點評:本題考查學生靈活運用同角三角函數間的基本關系及兩角差的正弦函數公式進行化簡求值的能力,學生做題時的突破點是正弦和余弦函數的值域都為[-1,1].

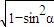 =
=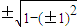 =0,sinβ=
=0,sinβ=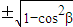 =
=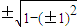 =0;
=0;

 閱讀快車系列答案
閱讀快車系列答案