
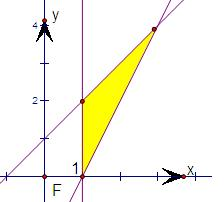
 解:先根據約束條件畫出可行域,
解:先根據約束條件畫出可行域,

 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案 海淀課時新作業金榜卷系列答案
海淀課時新作業金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中數學 來源: 題型:
| x+y |
| 1+xy |
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 用特征性質描述法表示圖中陰影部分的點(含邊界上的點)組成的集合M是
用特征性質描述法表示圖中陰影部分的點(含邊界上的點)組成的集合M是
|
|
|
|
查看答案和解析>>
科目:高中數學 來源:2012-2013學年四川省成都七中高一(上)期中數學試卷(解析版) 題型:解答題
 ;
; ,判斷是否有h(x)∈M,說明理由;
,判斷是否有h(x)∈M,說明理由; ,求函數
,求函數 的所有零點.
的所有零點.查看答案和解析>>
科目:高中數學 來源:2012-2013學年四川省成都七中高一(上)期中數學試卷(解析版) 題型:解答題
 ;
; ,判斷是否有h(x)∈M,說明理由;
,判斷是否有h(x)∈M,說明理由; ,求函數
,求函數 的所有零點.
的所有零點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com