【題目】如圖，在平面直角坐標系
中，橢圓
： 
的離心率為
，以原點為圓心，橢圓
的短半軸長為半徑的圓與直線
相切.
（1）求橢圓
的方程；
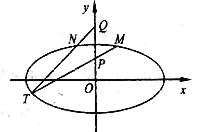
（2）已知點
，設
是橢圓
上關于
軸對稱的不同兩點，直線
與
相交于點
，求證：點
在橢圓上.
A加金題 系列答案
全優測試卷系列答案科目：高中數學 來源： 題型：
【題目】已知直線l1的方程為3x+4y﹣12=0．
（1）若直線l2與l1平行，且過點（﹣1，3），求直線l2的方程；
（2）若直線l2與l1垂直，且l2與兩坐標軸圍成的三角形面積為4，求直線l2的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點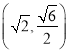
與點
都在橢圓
上.
（1）求橢圓
的方程；
（2）若
的左焦點、左頂點分別為
，則是否存在過點
且不與
軸重合的直線
(記直線
與橢圓
的交點為
)，使得點
在以線段
為直徑的圓上；若存在，求出直線
的方程；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】桑基魚塘是某地一種獨具地方特色的農業生產形式，某研究單位打算開發一個桑基魚塘項目，該項目準備購置一塊
平方米的矩形地塊，中間挖成三個矩形池塘養魚，挖出的泥土堆在池塘四周形成基圍（陰影部分所示）種植桑樹，池塘周圍的基圍寬均為
米，如圖，設池塘所占總面積為
平方米．
（Ⅰ）試用
表示．
（Ⅱ）當取何值時，才能使得最大？并求出的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
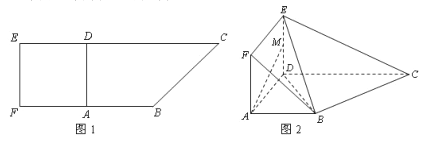
【題目】如圖 1，在直角梯形
中， 
，且
．現以
為一邊向形外作正方形
，然后沿邊
將正方形
翻折，使
平面與平面
垂直， 
為
的中點，如圖 2．
（1）求證： 
平面
；
（2）求證： 
平面
；
（3）求點
到平面
的距離.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的兩個焦點分別為
， 
，離心率為
，且過點
．
（
）求橢圓
的標準方程．
（
）
、
、
、
是橢圓
上的四個不同的點，兩條都不和
軸垂直的直線
和
分別過點
， 
，且這條直線互相垂直，求證： 
為定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在女子十米跳臺比賽中，已知甲、乙兩名選手發揮正常的概率分別為0.9，0.85，求：
(1)甲、乙兩名選手發揮均正常的概率；
(2)甲、乙兩名選手至多有一名發揮正常的概率；
(3)甲、乙兩名選手均出現失誤的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
